Team:Evry/LogisticFunctions
From 2013.igem.org
| Line 25: | Line 25: | ||
<h2>Differential form:</h2> | <h2>Differential form:</h2> | ||
| - | <p>Let the following be a Cauchy problem: | + | <p>Let the following be a Cauchy problem:<br/> |
y: x → y(x) a real function | y: x → y(x) a real function | ||
| Line 32: | Line 32: | ||
</p> | </p> | ||
| - | <p>The solution of this Cauchy problem is as below: | + | <p>The solution of this Cauchy problem is as below:<br/> |
y(x) = K/(1+(K/p – 1)*e^-bx) | y(x) = K/(1+(K/p – 1)*e^-bx) | ||
| Line 38: | Line 38: | ||
<p>Here is our logistic function. Yet, differential equations are not always time-related. | <p>Here is our logistic function. Yet, differential equations are not always time-related. | ||
| - | Let x be a temporal function, and y be a x-related logistic function. In order to integrate y into a temporal ODE, we need to write it differently: | + | Let x be a temporal function, and y be a x-related logistic function. In order to integrate y into a temporal ODE, we need to write it differently:<br/> |
dy/dx = by(x(t))(1 – y(x(t))/K) | dy/dx = by(x(t))(1 – y(x(t))/K) | ||
| Line 44: | Line 44: | ||
</p> | </p> | ||
| - | <p>And so: | + | <p>And so:<br/> |
dy/dt = dx/dt * by(x(t))(1 – y(x(t))/K) | dy/dt = dx/dt * by(x(t))(1 – y(x(t))/K) | ||
| - | If t → x(t) is a continuous real function, then: | + | If t → x(t) is a continuous real function, then:<br/> |
y(x(t)) = y(t) | y(x(t)) = y(t) | ||
| - | Finally, | + | Finally,<br/> |
dy/dt = dx/dt * by(1 – y/K) | dy/dt = dx/dt * by(1 – y/K) | ||
Revision as of 15:15, 29 September 2013
Logistic functions :
When we started to model biological behaviors, we realised very soon that we were going to need a function that simulates a non-exponential evolution, that would include a simple speed control and a maximum value. A smooth step function.
Such functions, named logistic functions were introduced around 1840 by M. Verhulst.
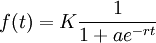
These functions looked perfect, but we needed more control : we needed to set a starting value and a precision.

Parameters:
- Q : Magnitude.
The limit of g as x approaches infinity is Q. - d : Threshold.
The value of x from which we consider the start of the phenomenon. - p : Precision.
g(d)=Q*p Since the function never reaches 0 nor Q, we have to set an approximation for 0 or Q. - k : Efficiency.
This parameter influences the length of the phenomenon.

Differential form:
Let the following be a Cauchy problem:
y: x → y(x) a real function
y' = b*y*(1-y/K)
y(0) = p
The solution of this Cauchy problem is as below:
y(x) = K/(1+(K/p – 1)*e^-bx)
Here is our logistic function. Yet, differential equations are not always time-related.
Let x be a temporal function, and y be a x-related logistic function. In order to integrate y into a temporal ODE, we need to write it differently:
dy/dx = by(x(t))(1 – y(x(t))/K)
<=>( dy/dt)/(dx/dt) = by(x(t))(1 – y(x(t))/K)
And so:
dy/dt = dx/dt * by(x(t))(1 – y(x(t))/K)
If t → x(t) is a continuous real function, then:
y(x(t)) = y(t)
Finally,
dy/dt = dx/dt * by(1 – y/K)
References:
 "
"













