Team:Colombia Uniandes/Stochastic
From 2013.igem.org
Stochastic
The biochemical reactions carried out in living systems, specifically in cells, are in general stochastic processes. Transcription, signaling networks and systems within a cell can be modeled and simulated in time as Markovian processes. Gillespie algorithm (see references) gives a stochastic simulation method of these kinds of phenomena and offers a good resolution with an efficient use of computational resources. The advantage of this kind of modeling is that the differential equations that we use in the deterministic model can also be used in the stochastic model.To develop the stochastic model for both projects the following assumptions were made:
- Only one event happens at each time
- The union of the ribosome and the RNA is considered a permanent bond, not intermittent.
- Transcription and Translation are modelled as a single event
Glucocorticoid Detection System
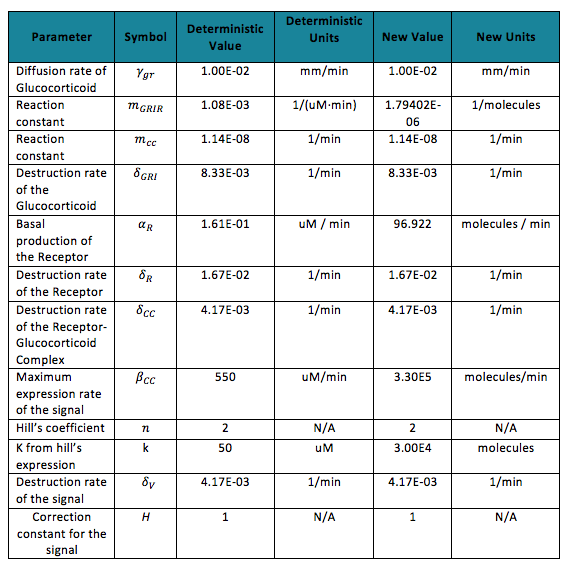
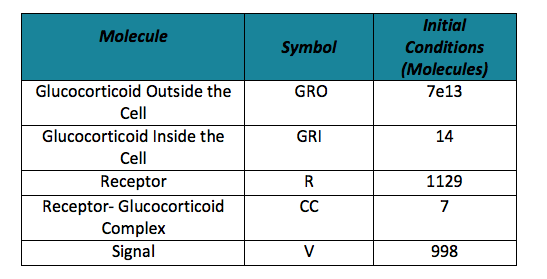
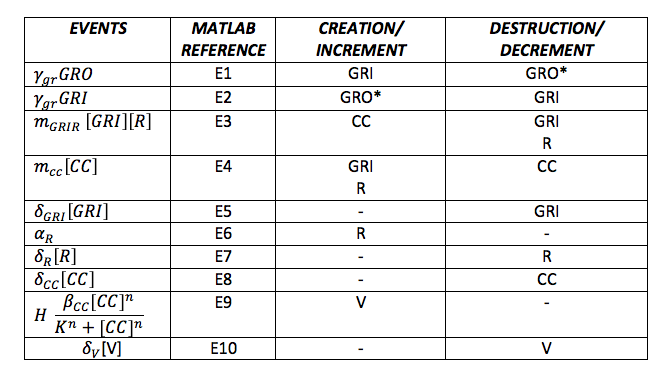
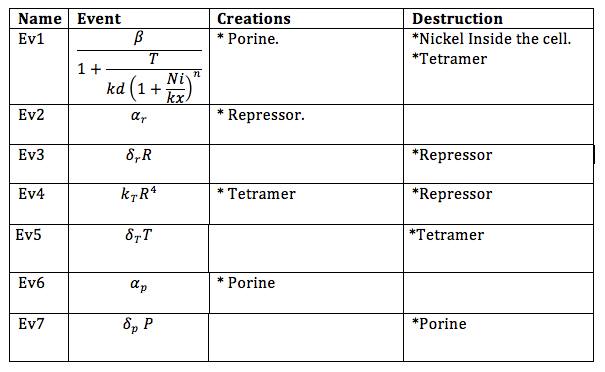
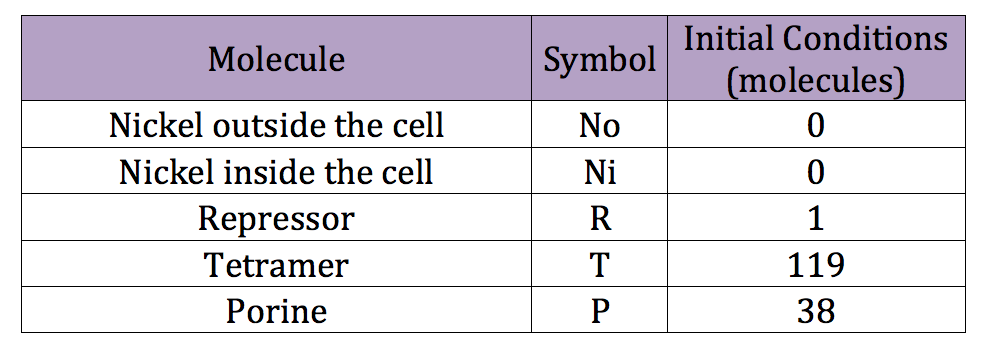
To do the adequate stochastic simulation for the glucocorticoid detection system, units should be defined in terms of molecules. For this purpose we estimate an average cell volume of 10e-15liters. The Table below has the parameters of the deterministic model and the parameters expressed in terms of number of molecules, which were used to obtain the initial conditions of each molecule type of our system. In order to obtain the initial conditions, which will in turn work as the baseline of our system, we run conInd.m with the new parameters. The molecules of our system are shown with its respective symbol in Table 2 along with the values obtained for the initial conditions In the simulation, either the creation/increment or destruction/decrement of each of the molecules depends on the occurrence of an event as shown on the Table 3 this information was analyzed from the differential equations proposed for the model.(See [https://2013.igem.org/Team:Colombia_Uniandes/Modeling Differential Equations]) Taking into account that GRO glucocorticoids outside the cell will be substantially more than inside of the cell, the value for this molecule will be considered constant throughout the model and will be dependent on the impulse function.Results
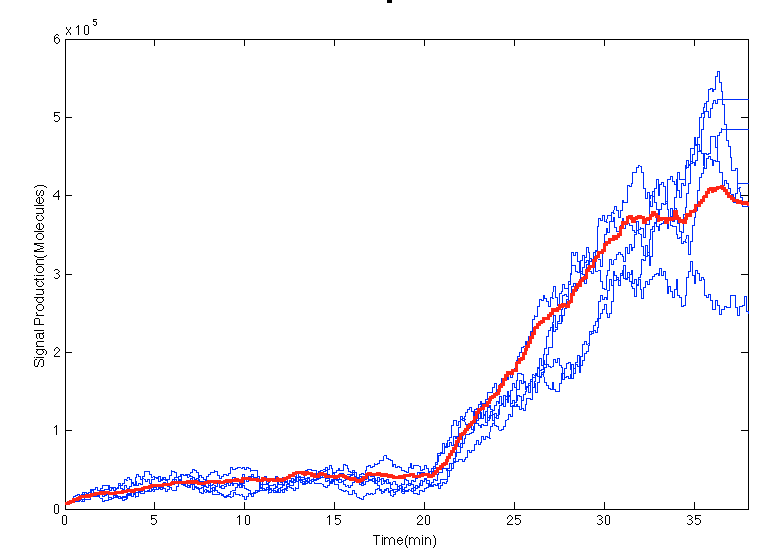
In the scripts an impulse of glucocorticoid is created at 20min. In the Figure below before the impulse of stress levels of GC the system was in steady state. After the impulse the signal increases in the cells an 15 minutes later it seems to estabilize.
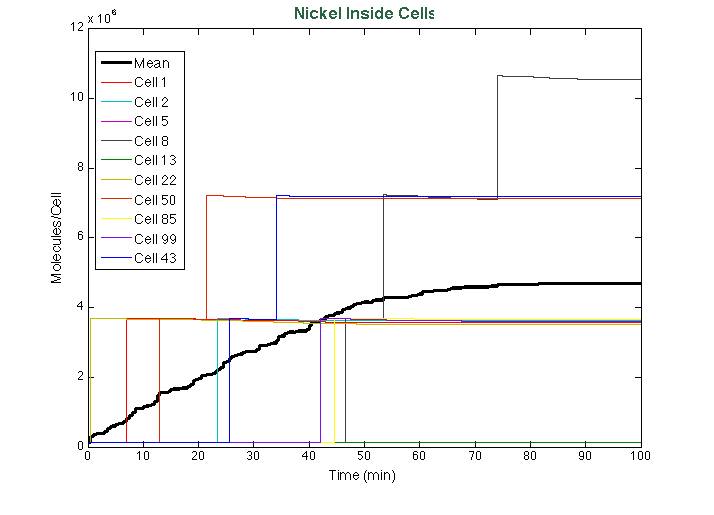
Nickel removal system
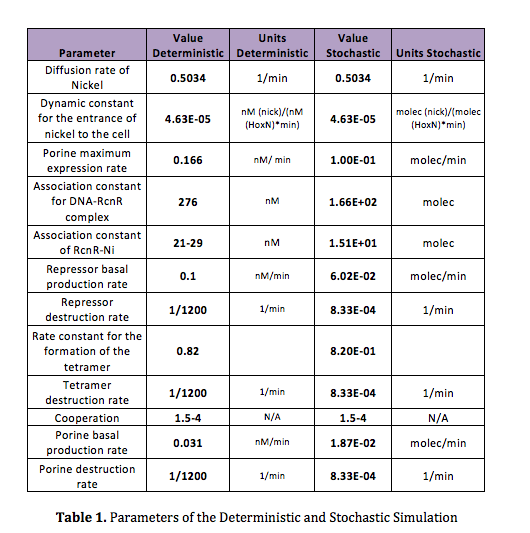
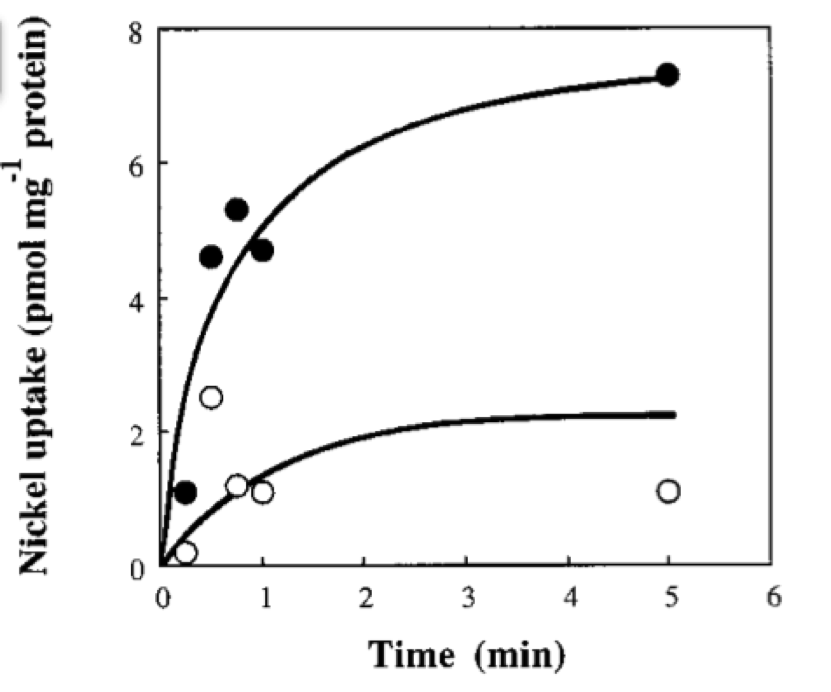
In order to do the simulation for our nickel uptake system, we must start defining the parameters of the model in the correct units. For our purposes and the algorithm’s requirements, we need units of molecules per unite of time (in our case, minutes). In the following table we show the parameters used for deterministic simulation and the stochastic parameters. The new parameters where obtained by using Avogadro's number (6.02e23 molecules per mole) and an average cell volume of 10e-15 liters.If we neglect the union of the nickel ion with the repressor, we can assume that nickel concentration in each cell is a function of the quantity of porine in the cell membrane and time. This function, known to be exponential, can be obtained by using an interpolation of data found in publications (Wolfram, Friedrich, & Eitinger, 1995). We could use a fitting function to describe the nickel uptake in the cell through time. However, we noticed that after 5 minutes, the curve reaches a steady state value. Given that we are not modeling the creation of mRNA and then the transcription (we are making an approximation for our time interests and computationally efficiency) we have a ~5min resolution. With this time resolution, it won’t matter if we fit the curve of figure 1 with higher detail. So we do an approximation based on the steady state of about 7pmolNickel/mgPorine
We can run a similar code used in the deterministic simulation to obtain reasonable initial conditions for the stochastic simulation. However this time we introduce the new, adequate parameters. The initial conditions obtained are listed in the next table
After running the scripts, these were the results of the simulation:
References
- Gillespie, D. T. (2007). Stochastic Simulation of Chemical Kinetics. Annual Review of Physical Chemistry, 58(1), 35–55. doi:10.1146/annurev.physchem.58.032806.104637.
- Wolfram, L., Friedrich, B., & Eitinger, T. (1995). The Alcaligenes eutrophus protein HoxN mediates nickel transport in Escherichia coli. Journal of bacteriology, 177(7), 1840–3. Retrieved from http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=176814&tool=pmcentrez&rendertype=abstract.
 "
"