Team:ETH Zurich/Modeling/Analytical Approximations
From 2013.igem.org
| Line 49: | Line 49: | ||
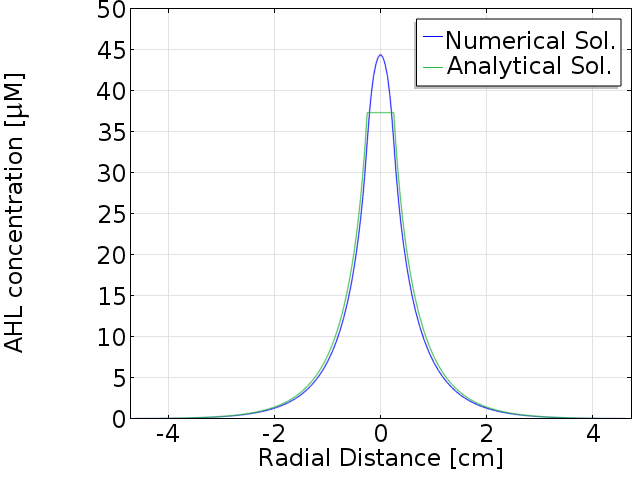
[[File:AHLss analytical.png|600px|center|thumb|<b>Figure 1:</b> Analytical approximation and numerical solution]] | [[File:AHLss analytical.png|600px|center|thumb|<b>Figure 1:</b> Analytical approximation and numerical solution]] | ||
| - | <br clear="all"/> | + | |
| + | <br clear="all" /> | ||
| + | <html> | ||
| + | </div> | ||
| + | </html> | ||
{:Team:ETH_Zurich/Templates}} | {:Team:ETH_Zurich/Templates}} | ||
| Line 58: | Line 62: | ||
<p align = "justify">In order to reduce the calculations, the current model with 6 species can be simplified to 3 species. Basically, proteins that are constitutively produced and linearly degraded can be assumed as constants, which is the case for LuxI and LuxR. Regarding the complex LuxR/AHL, we can expressed production of the output proteins drove by AHL. Thus, we have senders cells producing AHL and receiver cells processing the signal producing two colour outputs. </p> | <p align = "justify">In order to reduce the calculations, the current model with 6 species can be simplified to 3 species. Basically, proteins that are constitutively produced and linearly degraded can be assumed as constants, which is the case for LuxI and LuxR. Regarding the complex LuxR/AHL, we can expressed production of the output proteins drove by AHL. Thus, we have senders cells producing AHL and receiver cells processing the signal producing two colour outputs. </p> | ||
| - | |||
{{:Team:ETH_Zurich/templates/footer}} | {{:Team:ETH_Zurich/templates/footer}} | ||
Revision as of 15:10, 27 October 2013
Contents |
Steady State AHL Gradient Approximation
In the reaction-diffusion model we have formalized the gradient establishment and we solved the resulting partial differential equation numerically. Now, the aim is to derive a suitable analytical approximation for a single mine colony.
Kolmogorov-Petrovsky-Piskounov Equation
A reaction–diffusion equation concerning the concentration of a single molecule in one spatial dimension is known as the Kolmogorov-Petrovsky-Piskounov Equation. In our case, the equation for AHL has the following general structure:
\begin{align} \frac{\partial AHL(x,t)}{\partial t} = Diff(AHL(x,t),x) + R(AHL(x,t)) \end{align}
We were interested in the AHL gradient that can be established by a single colony ( located at $x = 0$) on an agar plate, ending up with a less general form of the reaction-diffusion model for AHL:
\begin{align} \frac{\partial AHL}{\partial t} = C_{agar} \cdot D_{AHL} \frac{\partial^2 AHL}{\partial x^2} - d_{AHL,e} \cdot [AHL] \end{align}
As boundary condition, we considered that the concentration at the mine colony stays constant, i.e. we are assuming cells are at the steady state:
\begin{align} [AHL](x=0,t) = [AHL]_{MineCell,ss} = \frac{\alpha_{AHL} \cdot [LuxI]_{ss}} {d_{AHL,i}+\eta \cdot \left(1-\frac{\eta_{ext}}{d_{AHL,e}+\eta_{ext}}\right)} \end{align}
Solution at the steady state
To solve the KPP equation for the steady state, we set to zero the time derivative:
\begin{align} \frac{\partial AHL}{\partial t} = C_{agar} \cdot D_{AHL} \frac{\partial^2 AHL}{\partial x^2} - d_{AHL,e} \cdot [AHL] = 0 \end{align} \begin{align} \frac{\partial^2 AHL}{\partial x^2} = \frac{d_{AHL,e}} {C_{agar} \cdot D_{AHL}} \cdot [AHL] \end{align}
This ordinary differential equation can be solved, integrating wrt. to x twice:
\begin{align} [AHL] = [AHL]_{MineCell,ss} \cdot e^{-\sqrt{\frac{d_{AHL,e}} {C_{agar} \cdot D_{AHL}}} \cdot x} \end{align}
Comparison with numerical solution
{:Team:ETH_Zurich/Templates}}
Search for an optimal promoter mutant
For the case of 2 neighbouring mines, we need two introduce a second promoter with a different sensitivity towards the complex LuxR/AHL. Experimentally the problem was addressed by constructing a library of promoter mutants. From the model we wanted to evaluate the mutants in order to predict which one could be the best.
In order to reduce the calculations, the current model with 6 species can be simplified to 3 species. Basically, proteins that are constitutively produced and linearly degraded can be assumed as constants, which is the case for LuxI and LuxR. Regarding the complex LuxR/AHL, we can expressed production of the output proteins drove by AHL. Thus, we have senders cells producing AHL and receiver cells processing the signal producing two colour outputs.
 "
"