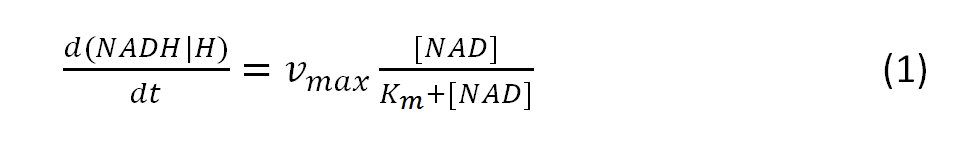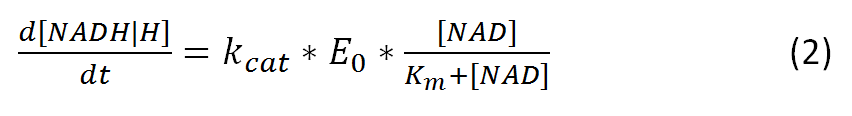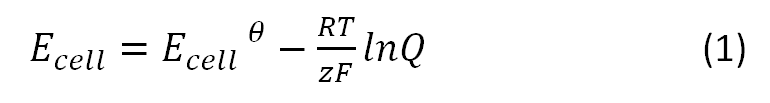Team:Bielefeld-Germany/Modeling
From 2013.igem.org
| Line 80: | Line 80: | ||
<br><br><br><br> | <br><br><br><br> | ||
| + | ==Intermediates== | ||
| + | <p align="justify"> | ||
| + | The electrons that will be eventually transferred to the anode are generated during the biochemical processes within the bacterial cell. The central pathway in E.coli is the glycolysis and one of its bottleneck reactions is the reaction catalyzed by the [http://www.genome.jp/dbget-bin/www_bget?ec:1.2.1.12 Glyceraldehyde 3-phosphate dehydrogenase (GAP-DH)]. In the course of this reaction the NAD+ is transformed to the reducing intermediate NADH/H+. Thus this intermediate takes part in the electron flow needed for the generation of electricity. | ||
| + | The resulting amount of the intermediate NADH/H can be calculated with the modeled Michaelis-Menten equation: <br> | ||
| + | </p> | ||
| + | [[File:Bielefeld-germany-model-inter-reaction1.PNG|500px|center]] | ||
| + | |||
| + | |||
| + | , where ''vmax'' is the maximum rate achieved by the system | ||
| + | and ''Km'' describes the substrate concentration at the half-maximal rate, that can be achieved by the system.<br> | ||
| + | |||
| + | |||
| + | Further the vmax can be also represented as: | ||
| + | |||
| + | |||
| + | [[File:Bielefeld-germany-model-inter-bild2.PNG|200px|center]] | ||
| + | |||
| + | |||
| + | , where ''kcat'' represents the rate-limiting turnover number | ||
| + | and ''E0'' represents the enzyme concentration. | ||
| + | The resulting equation, alternative to (1), would be: | ||
| + | |||
| + | |||
| + | [[File:Bielefeld-germany-model-inter-reaction2.PNG|500px|center]] | ||
| + | |||
| + | |||
| + | <p align="justify"> | ||
| + | The data of the kinetics have been obtained from the internet database [http://www.brenda-enzymes.org/php/result_flat.php4?ecno=1.2.1.12 BRENDA]. For ''E.coli'' the ''Km'' value for the NAD as a substrate is 0.045 for the wild-type enzyme. Unfortunately neither the turnover number nor the ''vmax'' for this organism could be found. Also the in depth research of the enzyme GAP-DH on the maximum rate of the reaction gave no satisfactory results – the only found value of vmax was the one from the ciliate Tetrahymena thermophile and was obtained from the method, where the GAP-DH was inhibited by stress reagents. Hence, there are two possible solutions how the model could be assessed: | ||
| + | </p> | ||
| + | |||
| + | |||
| + | *Applying the turnover number of another bacteria for the wild-type enzyme (e.g.: ''Bacillus subtilis'' with the ''kcat'' = 70 [1/s]) OR | ||
| + | *Applying the ''Vmax'' for the ''T. thermophile'' ([http://abbs.oxfordjournals.org/content/44/6/527.long1 Errafiy, Soukri , 2012]) | ||
| + | |||
| + | |||
| + | More plausible is the first application as the organism, to which the data referred, is closer related to E.coli and the data has been taken for the wild-type enzyme. Furthermore, ''B. subtilis'' has been cultivated under standard conditions and the activity of the enzyme hasn’t been influenced by any additional environmental factor. | ||
| + | |||
| + | ==Simulation== | ||
| + | |||
| + | The values ''k<sub>cat</sub>'' and ''K<sub>m</sub>'' obtained as mentioned above were applied in the simulation of the | ||
| + | production of NADH. The start concentration of the enzyme GAP-DH was set at 10 µM and the simulation time span at 10 sec. | ||
| + | The simulation was performed for five different NAD<sup>+</sup> concentrations: 10 µM, 20 µM, 100 µM, 500 µM and 1 M. | ||
| + | The MATLAB source code can be obtained as .m file [https://static.igem.org/mediawiki/2013/5/56/Bielefeld-germany-model-inter-matlab-code.m here]. | ||
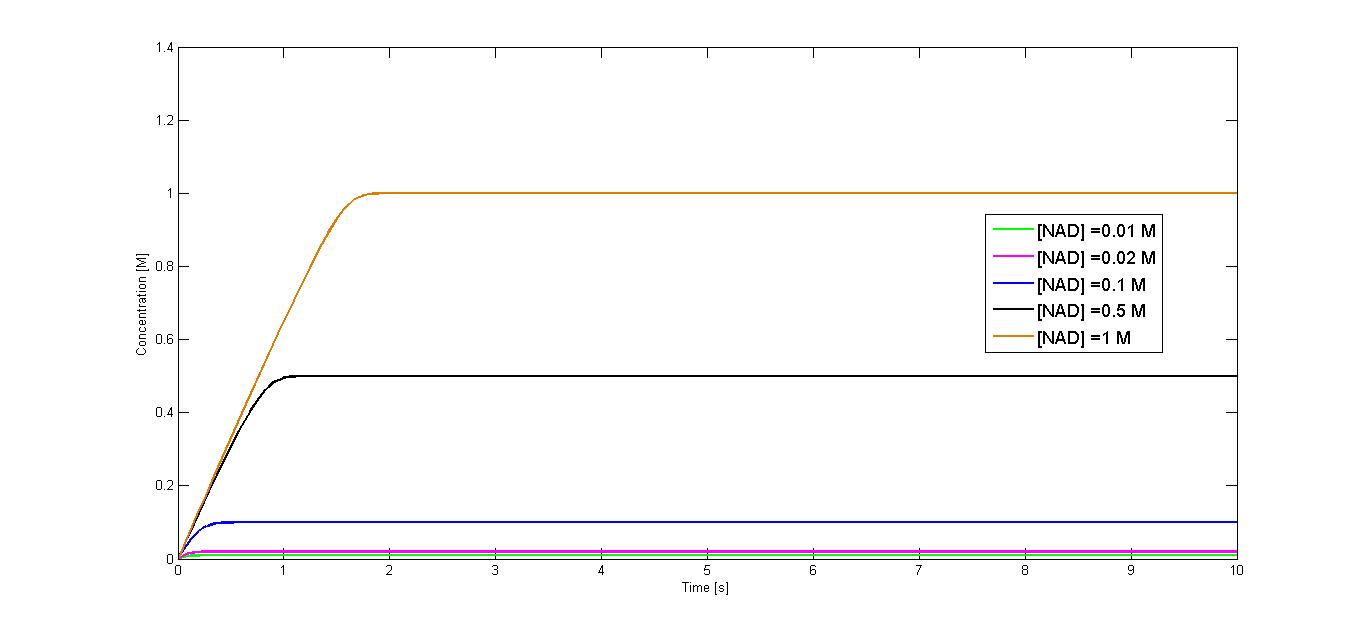
| + | Exemplary curves of the concentration change over time for the start NAD<sup>+</sup> concentration of 10 µM and 1 M are shown in figure 1 and figure 2 respectively. The curves showing the concentration change of the producht NADH for all simulated start concentration of subtrate are shown in the figure 3. | ||
| + | <br><br> | ||
| + | [[File:Bielefeld-germany-model-inter-diag-2.jpg|500px|center|thumb|'''Figure 1''': The curve of concentration change for the substrate NAD<sup>+</sup> and product NADH . Start concentration of substrate set at 10 µM]] | ||
| + | <br> | ||
| + | [[File:Bielefeld-germany-model-inter-diag-1.jpg|500px|center|thumb|'''Figure 2''': The curve of concentration change for the substrate NAD<sup>+</sup> and product NADH. Start concentration of substrate was set at 1 M]] | ||
| + | <br> | ||
| + | |||
| + | [[File:Bielefeld-germany-model-inter-diag-all.jpg|500px|center|thumb|'''Figure 3''': The curve of concentration change of the product NADH within 10 seconds for different substrate start concentrations [NAD].]] | ||
| + | <br><br> | ||
| + | [[File:Bielefeld-germany-model-inter-diag-all2.PNG|500px|center|thumb|'''Figure 3''': The curve of concentration change of the product NADH within 10 seconds for different substrate start concentrations [NAD].]] | ||
| + | <br><br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Mediator Reduction== | ||
| + | <p align="justify"> | ||
| + | In Microbial Fuel Cell microorganisms provide the electrons for the anode from the oxidation of the substrate(s) in the intracellular metabolic pathways. | ||
| + | The transfer of the electrons to electrodes has been demonstrated for several species, though this process is inefficient as far as Coulombic yield and current generation are concerned [A]. | ||
| + | Hence, the application of the electrochemical mediators is essential for the construction of Microbial Fuel Cell. | ||
| + | |||
| + | Mediators are usually small water-soluble molecules, which are capable of undergoing the redox transformations. The mediator acts as an electron shuttle, enhancing the kinetics of the electron transfer. This approach has been proven to be generally quite successful and many substances were tested for their potential as electron shuttle.<br> | ||
| + | <br> | ||
| + | There are two classes of mediators, the endogenous and the exogenous mediator. The endogenous mediators are generated by the bacteria and can be secreted to the medium and then be reduced at the electrode. The exogenous mediators are the redox molecules that are chemically synthesized and must be added into the anode chamber of the Microbial Fuel Cell, in order to enable electron transfer from bacterial metabolic pathways to the anode. <br> | ||
| + | <br> | ||
| + | Therefore, the anodic performance dependents not only on the nature and the rate of the metabolism, but on the nature and the rate of electron transfer from the mediator to the anode as well. | ||
| + | Several exogenous mediators have been already studied in regard to their effect on electron transfer and so their impact on the electricity generation. Among those mediators are methylene blue (MB), neutral red (NR), thionin, ferricyanide, humic acid or methyl viologen. | ||
| + | In our model we modelled the influence of the three of the mediators: <br><br> | ||
| + | * N-methyl phenazine (NMP)methosulfate, | ||
| + | * 1-methoxy-5-methyl phenazine (MNMP) methosulfate and | ||
| + | * Meldola Blue (MB ) | ||
| + | </p> | ||
| + | <br><br><br><br> | ||
| + | == '''Reaction Kinetics''' == | ||
| + | |||
| + | In contrast to the first bottle neck reaction of our model, which has been described as the Michaelis-Menten reaction, the redox reaction between the bacterial metabolites and the oxidized mediator can be considered as a first order reaction: | ||
| + | |||
| + | [[File:Bielefeld-germany-model-reduction-1.PNG|300px|center]] | ||
| + | |||
| + | |||
| + | The kinetic properties of the electrocatalytic oxidation of NADH and reduction of the soluble mediator, regarding rate constants were studied by cyclic voltammetry and chronoamperometry [B]. | ||
| + | The measured rates are shown in the table 1: | ||
| + | |||
| + | [[File:Bielefeld-germany-model-reduction-table1.PNG|500px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Mediator Oxidation== | ||
| + | <p align="justify"> | ||
| + | In a third electrochemical reaction the reduced mediator is regenerated at the electrode.This electrochemical oxidation at the anode surface occurs as shown in equation: <br><br> | ||
| + | |||
| + | [[File:Bielefeld-germany-model-oxid-reaction-1.PNG|300px|center]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ,where M<sub>red</sub> is the reduced mediator and <br> | ||
| + | M<sub>ox</sub> the oxidized mediator. | ||
| + | <br> | ||
| + | Then the current output can be calculated based on formula according to the Faraday's law:<br> | ||
| + | |||
| + | [[File:Bielefeld-germany-model-oxid-reaction-2.PNG|250px|center]] | ||
| + | |||
| + | <br><br> | ||
| + | ,where I is the current density [A]<br> | ||
| + | [M<sub>red</sub>] is the concentration of reduced mediator in the chamber<br> | ||
| + | ''n'' is the number of electrons taking part in the electrode reaction,<br> | ||
| + | F is the Faradays constant (96 500 C) and <br> | ||
| + | k<sub>3</sub> is the reaction rate, mentioned above.<br> | ||
| + | |||
| + | </p> | ||
| + | <br> | ||
| + | ==Simulation== | ||
| + | <p align="justify"> | ||
| + | The value ''k<sub>3</sub>'' obtained as mentioned above was applied in the simulation of the current output in the final reaction of the three-reaction model. The start concentrations of the NAD<sup>+</sup> and oxidized mediator were set as in the simulations preformed for the proceeding reactions at 100 µM. The simulation time span was set for 60 sec. | ||
| + | The resulting plot for the mediator '''MB''' is shown in the Figure 1, below: | ||
| + | |||
| + | |||
| + | [[File:Bielefeld-germany-model-oxid-diagramm-MB-01.png|600px|center|thumb|'''Figure 1''': Curves for the current output, fluxes of concentration of the intermediates. Simulation performed for the start concentration of both NAD<sup>+</sup> and oxidized mediator at 100 µM.]] | ||
| + | |||
| + | |||
| + | Further simulation has been performed for four different start concentrations of the oxidised mediator in order to investigate how varying start concentration influence the current output. The concentrations were set at 10 µM, 50 µM, 100 µM and 500 µM. The time span was set at 30 sec. The curves of the current outputs are presented in the Figure 2. | ||
| + | |||
| + | [[File:Bielefeld-germany-model-oxid-diagramm-MB-02.png|600px|center|thumb|'''Figure 1''': Curves for the current output, fluxes of concentration of the intermediates. Simulation performed for the start concentration of both NAD<sup>+</sup> and oxidized mediator at 100 µM.]] | ||
| + | |||
| + | |||
| + | The MATLAB source code for both simulations can be obtained [https://static.igem.org/mediawiki/2013/5/56/Bielefeld-germany-model-inter-matlab-code.m here] and [https://static.igem.org/mediawiki/2013/5/56/Bielefeld-germany-model-inter-matlab-code.m here].<br> | ||
| + | |||
| + | |||
| + | Analogous simulations have been performed for the mediator '''NMP'''. As the reaction rate ''k<sub>3</sub>'' specific of the could not be accessed, the value specific for the mediator '''MB''' was applied. | ||
| + | The according .m files with MATLAB source code can be downloaded from [https://static.igem.org/mediawiki/2013/5/56/Bielefeld-germany-model-inter-matlab-code.m here] and [https://static.igem.org/mediawiki/2013/5/56/Bielefeld-germany-model-inter-matlab-code.m here]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Overview== | ||
| + | <p align="justify"> | ||
| + | The Microbial Fuel Cell will be subjected to numerous parameters, which will heavily influence its performance. Therefore, there is a need to inquiry the impact of those parameters on the efficiency of the system. In our approach we focused on how the reduction potential of the given mediators depends on two parameters, namely the pH value and the temperature. | ||
| + | |||
| + | All values were calculated based on the [http://en.wikipedia.org/wiki/Nernst_equation Nernst equation], which describes the relation between the electromotive force of the full cell and the temperature or the pH-value: | ||
| + | </p> | ||
| + | |||
| + | |||
| + | [[File:Bielefeld-germany-model-optimal-Nernst.PNG|500px|center]]<br> | ||
| + | |||
| + | ==Optimal pH value== | ||
| + | <p align="justify"> | ||
| + | The following exogenous mediators were analyzed under varying pH-value: | ||
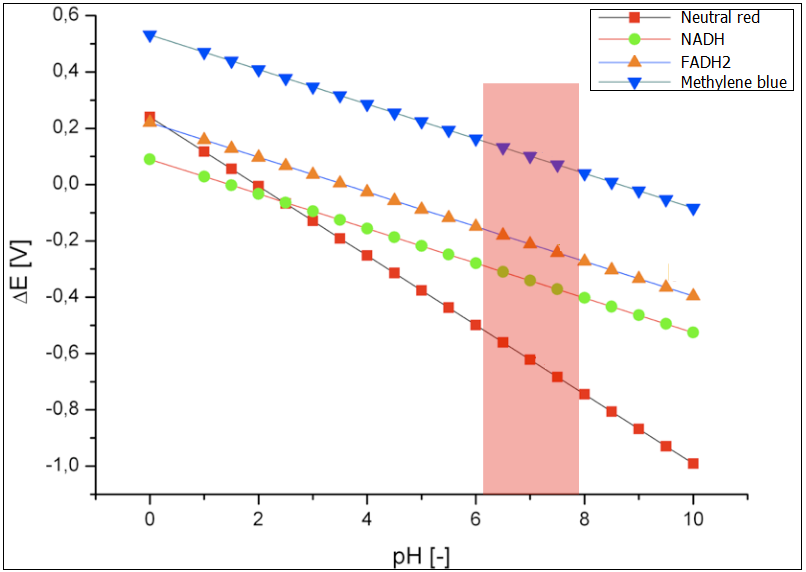
| + | Neutral red, NADH, FADH2 and Methylene blue. The results are presented in the Figure 1. The optimal conditions for the growth of ''E.coli'' have been marked in red. Methylene blue has been chosen as the proof of concept for the experimental examination of the fuel cell, after various initial tests. Hence, it has been in the focus of the modeling of the performance as well. <!--The modeling, based on the equation (1) provides the following results--> | ||
| + | |||
| + | The reduction potential for the optimal growth conditions for ''E.coli'', is between ~0.13 and ~0.8 V. The reduction potential for neutral red lies in this pH interval is between -0.4 and -0.7. This value is too low and would not lead to reduced performance of the fuel cell. The best electromotive force would be provided by the systems NADH and FADH2. | ||
| + | </p> | ||
| + | |||
| + | |||
| + | [[Image:Bielefeld-germany-model-optimal-ph3.png.png|500px|thumb|center|'''Figure 1:''' Reduction potential of different mediators related to the pH value in the chamber. ]] | ||
| + | |||
| + | |||
| + | ==Optimal temperature== | ||
| + | <p align="justify"> | ||
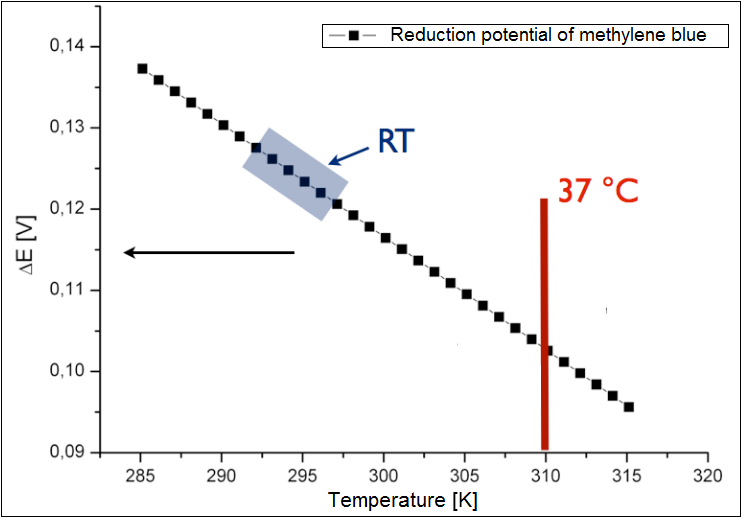
| + | The analysis was conducted only for an exogenous mediator methylene blue. The results have been shown in the figure 2 below. It could be shown, that the calculated reduction potential differs only slightly for the broad spectrum of the temperature, and all lies at about 0.1 V. Therefor the temperature is not the limiting parameter for the performance of the fuel cell. The charge at the optimal growth condition for E. coli (37 °C or 310 K) is ~0.13 . | ||
| + | </p> | ||
| + | |||
| + | |||
| + | [[Image:Bielefeld-germany-model-optimal-temp.png|500px|thumb|center|'''Figure 2:''' Calculated reduction potential of the methylene blue dependent on the temperature of the system]] | ||
| + | |||
| + | |||
| + | |||
| + | ==Combined calculations for the proof system== | ||
| + | <p align="justify"> | ||
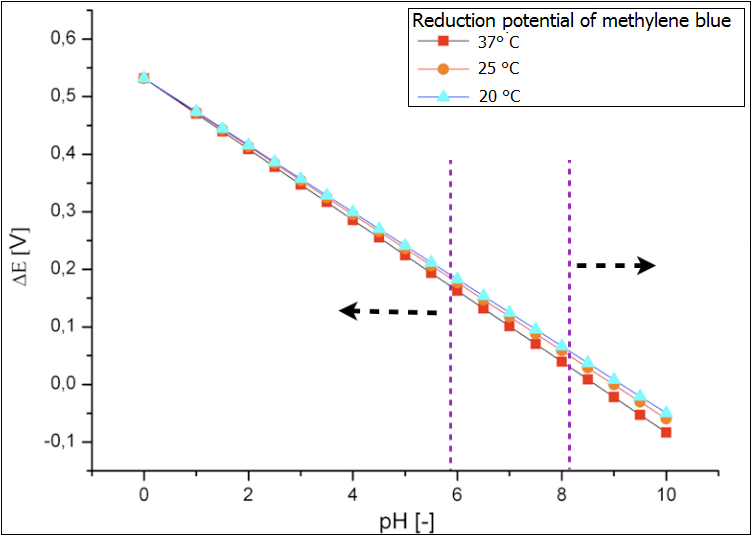
| + | Ultimately the analysis of the influence of both temperature and pH value on the reduction potential of the proof system methylene blue has been performed. Its results are depicted in the figure 3. Again it could be shown that the temperature does not affect the reduction potential and therefore the effectiveness of the fuel cell. In contrast the pH-value in the chamber should be monitored and kept at the values that correspond to the optimal growth condition of the E.coli cells. The values below 6 would lead to too high reduction potential via the accumulation of the fermentation products under anaerob cultivation and decreased efficiency. Too basic conditions in the chamber (above 8) would lead to oxidation of the glucose and to so-called Blue-Bottle-Effect. The performance of the fuel cell would be also worse. | ||
| + | </p> | ||
| + | |||
| + | |||
| + | [[Image:Bielefeld-germany-model-optimal-ph1.png|500px|thumb|center|'''Figure 3:''' Reduction potential of methylene blue dependent on pH value and temperature.]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==References== | ||
| + | *Errafiy N, Soukri A (2012). Purification and partial characterization of glyceraldehyde-3-phosphate dehydrogenase from the ciliate <i>Tetrahymena thermophila</i>. <i>[http://abbs.oxfordjournals.org/content/44/6/527.long Acta Biochimica et Biophysica Sinica, Volume 44]</i>(6), 527-534. | ||
<br><br><br><br> | <br><br><br><br> | ||
Revision as of 01:02, 29 October 2013
Modelling - Overview
Approach
In a Microbial Fuel Cell (MFC) the chemical energy is transformed into the electrical energy via a cascade of electrochemical reactions. Electrons are produced in the metabolic pathways and can be extracted from the cell and concentrated at the electrode by the electric potential differences. Alternatively the electrons can be transferred to the oxidized mediator molecules that transfer them further to the electrode. There is a variety of parameters and interactions that influence electricity generation. Therefore, there is the need to identify the bottleneck reactions and limiting factors. This approach reduces the complexity of the analysis and can give a deeper insight on the most important processes involved in the electricity generation.
In our theoretical analysis the focus was set to three bottleneck reactions involved in the electron flow from the metabolism of the bacterial cells to the cathode:
- Generation of intermediates NADH/H+ in the metabolic pathway of E.coli
- Reduction of oxidized mediators via the intermediate NADH
- Transfer of the electrons from reduced mediator to the electrode
Intermediates
The electrons that will be eventually transferred to the anode are generated during the biochemical processes within the bacterial cell. The central pathway in E.coli is the glycolysis and one of its bottleneck reactions is the reaction catalyzed by the [http://www.genome.jp/dbget-bin/www_bget?ec:1.2.1.12 Glyceraldehyde 3-phosphate dehydrogenase (GAP-DH)]. In the course of this reaction the NAD+ is transformed to the reducing intermediate NADH/H+. Thus this intermediate takes part in the electron flow needed for the generation of electricity.
The resulting amount of the intermediate NADH/H can be calculated with the modeled Michaelis-Menten equation:
, where vmax is the maximum rate achieved by the system
and Km describes the substrate concentration at the half-maximal rate, that can be achieved by the system.
Further the vmax can be also represented as:
, where kcat represents the rate-limiting turnover number
and E0 represents the enzyme concentration.
The resulting equation, alternative to (1), would be:
The data of the kinetics have been obtained from the internet database [http://www.brenda-enzymes.org/php/result_flat.php4?ecno=1.2.1.12 BRENDA]. For E.coli the Km value for the NAD as a substrate is 0.045 for the wild-type enzyme. Unfortunately neither the turnover number nor the vmax for this organism could be found. Also the in depth research of the enzyme GAP-DH on the maximum rate of the reaction gave no satisfactory results – the only found value of vmax was the one from the ciliate Tetrahymena thermophile and was obtained from the method, where the GAP-DH was inhibited by stress reagents. Hence, there are two possible solutions how the model could be assessed:
- Applying the turnover number of another bacteria for the wild-type enzyme (e.g.: Bacillus subtilis with the kcat = 70 [1/s]) OR
- Applying the Vmax for the T. thermophile ([http://abbs.oxfordjournals.org/content/44/6/527.long1 Errafiy, Soukri , 2012])
More plausible is the first application as the organism, to which the data referred, is closer related to E.coli and the data has been taken for the wild-type enzyme. Furthermore, B. subtilis has been cultivated under standard conditions and the activity of the enzyme hasn’t been influenced by any additional environmental factor.
Simulation
The values kcat and Km obtained as mentioned above were applied in the simulation of the
production of NADH. The start concentration of the enzyme GAP-DH was set at 10 µM and the simulation time span at 10 sec.
The simulation was performed for five different NAD+ concentrations: 10 µM, 20 µM, 100 µM, 500 µM and 1 M.
The MATLAB source code can be obtained as .m file here.
Exemplary curves of the concentration change over time for the start NAD+ concentration of 10 µM and 1 M are shown in figure 1 and figure 2 respectively. The curves showing the concentration change of the producht NADH for all simulated start concentration of subtrate are shown in the figure 3.
Mediator Reduction
In Microbial Fuel Cell microorganisms provide the electrons for the anode from the oxidation of the substrate(s) in the intracellular metabolic pathways.
The transfer of the electrons to electrodes has been demonstrated for several species, though this process is inefficient as far as Coulombic yield and current generation are concerned [A].
Hence, the application of the electrochemical mediators is essential for the construction of Microbial Fuel Cell.
Mediators are usually small water-soluble molecules, which are capable of undergoing the redox transformations. The mediator acts as an electron shuttle, enhancing the kinetics of the electron transfer. This approach has been proven to be generally quite successful and many substances were tested for their potential as electron shuttle.
There are two classes of mediators, the endogenous and the exogenous mediator. The endogenous mediators are generated by the bacteria and can be secreted to the medium and then be reduced at the electrode. The exogenous mediators are the redox molecules that are chemically synthesized and must be added into the anode chamber of the Microbial Fuel Cell, in order to enable electron transfer from bacterial metabolic pathways to the anode.
Therefore, the anodic performance dependents not only on the nature and the rate of the metabolism, but on the nature and the rate of electron transfer from the mediator to the anode as well.
Several exogenous mediators have been already studied in regard to their effect on electron transfer and so their impact on the electricity generation. Among those mediators are methylene blue (MB), neutral red (NR), thionin, ferricyanide, humic acid or methyl viologen.
In our model we modelled the influence of the three of the mediators:
- N-methyl phenazine (NMP)methosulfate,
- 1-methoxy-5-methyl phenazine (MNMP) methosulfate and
- Meldola Blue (MB )
Reaction Kinetics
In contrast to the first bottle neck reaction of our model, which has been described as the Michaelis-Menten reaction, the redox reaction between the bacterial metabolites and the oxidized mediator can be considered as a first order reaction:
The kinetic properties of the electrocatalytic oxidation of NADH and reduction of the soluble mediator, regarding rate constants were studied by cyclic voltammetry and chronoamperometry [B].
The measured rates are shown in the table 1:
Mediator Oxidation
In a third electrochemical reaction the reduced mediator is regenerated at the electrode.This electrochemical oxidation at the anode surface occurs as shown in equation:
,where Mred is the reduced mediator and
Mox the oxidized mediator.
Then the current output can be calculated based on formula according to the Faraday's law:
,where I is the current density [A]
[Mred] is the concentration of reduced mediator in the chamber
n is the number of electrons taking part in the electrode reaction,
F is the Faradays constant (96 500 C) and
k3 is the reaction rate, mentioned above.
Simulation
The value k3 obtained as mentioned above was applied in the simulation of the current output in the final reaction of the three-reaction model. The start concentrations of the NAD+ and oxidized mediator were set as in the simulations preformed for the proceeding reactions at 100 µM. The simulation time span was set for 60 sec. The resulting plot for the mediator MB is shown in the Figure 1, below:
Further simulation has been performed for four different start concentrations of the oxidised mediator in order to investigate how varying start concentration influence the current output. The concentrations were set at 10 µM, 50 µM, 100 µM and 500 µM. The time span was set at 30 sec. The curves of the current outputs are presented in the Figure 2.
The MATLAB source code for both simulations can be obtained here and here.
Analogous simulations have been performed for the mediator NMP. As the reaction rate k3 specific of the could not be accessed, the value specific for the mediator MB was applied.
The according .m files with MATLAB source code can be downloaded from here and here.
Overview
<p align="justify"> The Microbial Fuel Cell will be subjected to numerous parameters, which will heavily influence its performance. Therefore, there is a need to inquiry the impact of those parameters on the efficiency of the system. In our approach we focused on how the reduction potential of the given mediators depends on two parameters, namely the pH value and the temperature.
All values were calculated based on the [http://en.wikipedia.org/wiki/Nernst_equation Nernst equation], which describes the relation between the electromotive force of the full cell and the temperature or the pH-value:
Optimal pH value
The following exogenous mediators were analyzed under varying pH-value: Neutral red, NADH, FADH2 and Methylene blue. The results are presented in the Figure 1. The optimal conditions for the growth of E.coli have been marked in red. Methylene blue has been chosen as the proof of concept for the experimental examination of the fuel cell, after various initial tests. Hence, it has been in the focus of the modeling of the performance as well. The reduction potential for the optimal growth conditions for E.coli, is between ~0.13 and ~0.8 V. The reduction potential for neutral red lies in this pH interval is between -0.4 and -0.7. This value is too low and would not lead to reduced performance of the fuel cell. The best electromotive force would be provided by the systems NADH and FADH2.
Optimal temperature
The analysis was conducted only for an exogenous mediator methylene blue. The results have been shown in the figure 2 below. It could be shown, that the calculated reduction potential differs only slightly for the broad spectrum of the temperature, and all lies at about 0.1 V. Therefor the temperature is not the limiting parameter for the performance of the fuel cell. The charge at the optimal growth condition for E. coli (37 °C or 310 K) is ~0.13 .
Combined calculations for the proof system
Ultimately the analysis of the influence of both temperature and pH value on the reduction potential of the proof system methylene blue has been performed. Its results are depicted in the figure 3. Again it could be shown that the temperature does not affect the reduction potential and therefore the effectiveness of the fuel cell. In contrast the pH-value in the chamber should be monitored and kept at the values that correspond to the optimal growth condition of the E.coli cells. The values below 6 would lead to too high reduction potential via the accumulation of the fermentation products under anaerob cultivation and decreased efficiency. Too basic conditions in the chamber (above 8) would lead to oxidation of the glucose and to so-called Blue-Bottle-Effect. The performance of the fuel cell would be also worse.
References
- Errafiy N, Soukri A (2012). Purification and partial characterization of glyceraldehyde-3-phosphate dehydrogenase from the ciliate Tetrahymena thermophila. [http://abbs.oxfordjournals.org/content/44/6/527.long Acta Biochimica et Biophysica Sinica, Volume 44](6), 527-534.
 "
"