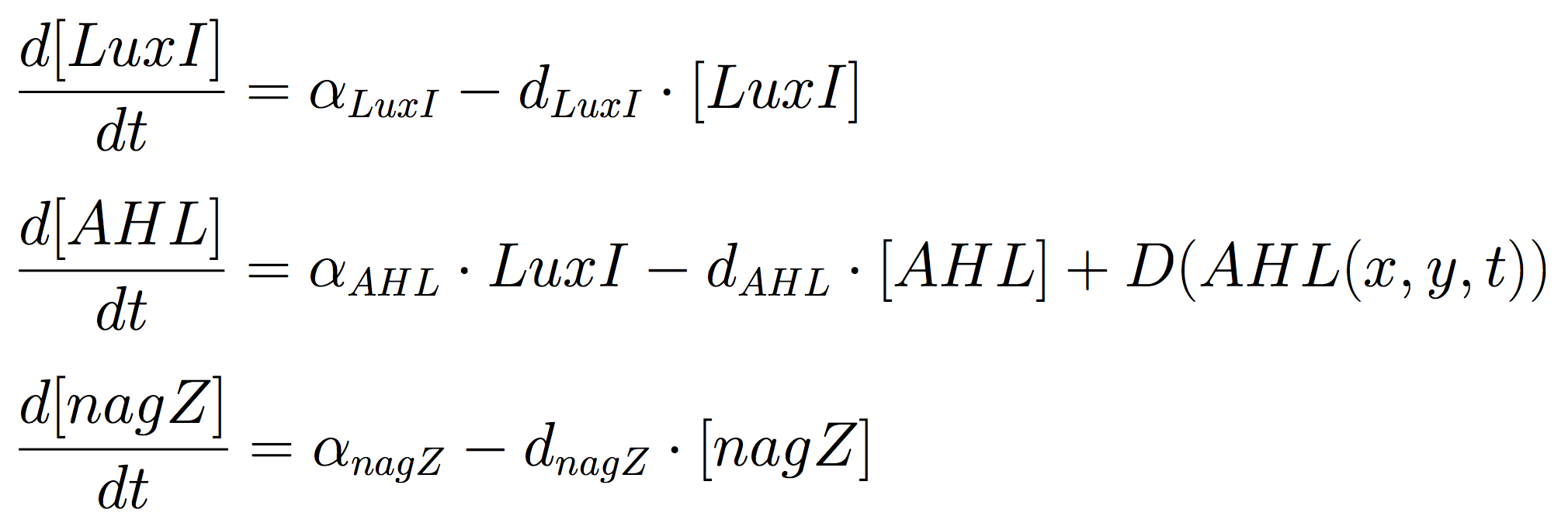Team:ETH Zurich/Modeling
From 2013.igem.org
| Line 19: | Line 19: | ||
<b>The digital bacterial-based minesweeper</b> | <b>The digital bacterial-based minesweeper</b> | ||
<br><br> | <br><br> | ||
| - | To explain how the concentration of AHL changes over time, we have to consider the influence of two processes: local chemical reactions and diffusion which causes the molecule to spread out over the agar plate. | + | To explain how the concentration of AHL changes over time, we have to consider the influence of two processes: local chemical reactions and diffusion which causes the molecule to spread out over the agar plate.<br> |
| - | [[File:Rxn_Diff_AHL.png|500px|right|thumb|''Figure 1: General partial differential equation for AHL reaction-diffusion. D(AHL( | + | [[File:Rxn_Diff_AHL.png|500px|right|thumb|''Figure 1: General partial differential equation for AHL reaction-diffusion. D(AHL('''r''',t),'''r''') is the diffusive term, R(AHL('''r''',t)) is the reaction term'']] |
| + | For the Diffusion, the equation is a partial differential equation (Fig. 2) which describes density fluctuations over time and space. | ||
[[File:Diff_AHL.png|500px|right|thumb|''Figure 2: Diffusive term for AHL'']] | [[File:Diff_AHL.png|500px|right|thumb|''Figure 2: Diffusive term for AHL'']] | ||
The change of the species concentrations in time is given by non-linear ordinary differential equations (ODEs), most of which follow Hill kinetics. The parameters we used in the model are derived from literature. In our model we consider that signalling molecules degrade at the same rate whether they are cytoplasmic or not. | The change of the species concentrations in time is given by non-linear ordinary differential equations (ODEs), most of which follow Hill kinetics. The parameters we used in the model are derived from literature. In our model we consider that signalling molecules degrade at the same rate whether they are cytoplasmic or not. | ||
Revision as of 12:10, 22 August 2013
The digital bacterial-based minesweeper
To explain how the concentration of AHL changes over time, we have to consider the influence of two processes: local chemical reactions and diffusion which causes the molecule to spread out over the agar plate.
For the Diffusion, the equation is a partial differential equation (Fig. 2) which describes density fluctuations over time and space.
The change of the species concentrations in time is given by non-linear ordinary differential equations (ODEs), most of which follow Hill kinetics. The parameters we used in the model are derived from literature. In our model we consider that signalling molecules degrade at the same rate whether they are cytoplasmic or not.
Mine Cells
The Mine Cells lead to the synthesis the signalling molecule, by constitutive expression of luxI gene. To reveal the nature of the cells, a coloured-substrate reaction is triggered upon addition of 5-Bromo-4-chloro-3-indoxyl-N-acetyl-beta-D-glucosaminide; given that the glycoside hydrolase NagZ is expressed constitutively.
The ODEs for the states involved in the sender module are given below:
Biosensors
Our Biosensor cells are engineered to respond differently to high and medium concentrations of AHL. This cells are capable of discriminate between the presence of 1 or 2 mine cells around them in the immediate vicinity. To accomplish this task, the enzymes involved in the coloured-substrate reaction are sensitive to different concentrations of the dimer LuxR-AHL (denoted as R).
 "
"