Team:ETH Zurich/GFP
From 2013.igem.org
| (111 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
{{:Team:ETH_Zurich/Templates/stylesheet}} | {{:Team:ETH_Zurich/Templates/stylesheet}} | ||
| - | + | <h1>Reaction-diffusion model: genetic circuit with GFP as reporter gene</h1> | |
| - | <h1>Reaction- | + | <p align="justify">'''Building on our first spatio-temporal model for AHL, we wanted to evaluate the model with experimental data, as a proof of concept. In order to detect the diffusible molecule, we designed an experiment with receiver cells containing GFP under the control of P<sub>LuxR</sub> promoter (wild type). Subsequently, we simulate a 2D spatio-temporal reaction-diffusion system including GFP under control of P<sub>LuxR</sub> with COMSOL Multiphysics.'''</p> |
| - | + | ||
<br clear="all"/> | <br clear="all"/> | ||
| - | < | + | <p align="center"><b>Video:</b> GFP expression levels over 11 hours, concentration in mol/m<sup>3</sup>. Distance between colonies: 1,5 cm.</p> |
| + | {{:Team:ETH Zurich/Templates/Video| | ||
| + | width=700px| | ||
| + | id=video2| | ||
| + | ratio=361/250| | ||
| + | srcMP4=<html>https://static.igem.org/mediawiki/2013/7/76/GFP_2.mp4</html> | ||
| + | |poster = <html>https://static.igem.org/mediawiki/2013/1/18/Gfp_video_11h.png</html> | ||
| + | }} | ||
<br> | <br> | ||
| - | |||
| - | + | <p align="justify">AHL diffuses in and out of mine cells, however the concentrations of species are time- and space-dependent. Thus the change of concentrations over time is given by system of non-linear partial differential equations (PDEs). Each equation represents the rate of change of species' continuous concentration as a sum of terms representing biological processes, such as production, degradation and regulation. The regulation is captured with Michaelis-Menten and Hill functions. For simplicity, we lump together specific cellular processes like transcription and translation, and do not model them explicitly. | |
| - | + | ||
| - | + | Our system consists of two types of genetically engineered colonies: (i) Mine Cells and (ii) Receiver Cells, that can be treated as modules that communicate only by a single molecule, AHL. Additionally, we include the decay of AHL while diffusing through the agar plate. <br></p> | |
| + | <br clear="all"/> | ||
| - | + | <h1>Mine colony </h1> | |
| - | < | + | <html><a id="MineColony" class="frog"></a></html> |
| - | + | <p align="justify">One protein is produced by mine colonies, LuxI, which is constitutively expressed and linearly degraded. Additionally, the synthesis of AHL is carried on by these sender cells; the product of ''luxI'' gene is directly involved in the synthesis of the signalling molecule, using as substrates ''S''-adenosylmethionine (SAM) and an acylated acyl carrier protein (ACP) from the fatty acid biosynthesis pathway (Schaefer ''et al.'', 1996). We assume precursor molecules are provided by the cell in non-limiting conditions. <br><br></p> | |
| + | The system of equations for the states involved in the sender module are given below: | ||
| - | [[ | + | \begin{align} |
| - | + | \frac{d[LuxI]}{dt} = \alpha_{LuxI} - d_{LuxI} \cdot [LuxI]\\ | |
| - | + | \end{align} | |
| + | |||
| + | \begin{align} | ||
| + | \frac{d[AHL]}{dt} = DF \cdot ( \alpha_{AHL} \cdot [LuxI] - d_{AHL,i} \cdot [AHL] ) + C_{agar} \cdot D_{AHL} \nabla^{2} [AHL] | ||
| + | \end{align} | ||
| + | <p align = "center"> System of Differential equations for mine colonies.</p> | ||
| - | |||
<br clear="all"/> | <br clear="all"/> | ||
| - | <h1> | + | <h1>Agar plate </h1> |
| + | <html><a id="Plate" class="frog"></a></html> | ||
| + | <p align="justify">In the agar plate no reactions take place; hence only two processes of interested are considered: (i) diffusion and (ii) decay of the diffusible signal, AHL (Eq 6). The equation for AHL in agar plate is given below: </p> | ||
| - | + | \begin{align} | |
| + | \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} [AHL] - d_{AHL,e} \cdot [AHL] | ||
| + | \end{align} | ||
| + | <p align = "center"> Processes taking place on the agar plate: diffusion and decay of AHL.</p> | ||
<br clear="all"/> | <br clear="all"/> | ||
| - | <h1> | + | <h1>Receiver colony </h1> |
| - | + | <p align="justify">Receiver cells are responsible for processing the signal sent by the mine cells. AHL acts as the input signal and the output is green fluorescence whose intensity correlates with the sensed AHL concentration by receiver cells; for this purpose GFP expression is under the control of pLux promoter. Once AHL molecules reach a non-mine colony, they can bind to LuxR protein, and the complex LuxR/AHL acts as a transcriptional activator. Therefore, this module works as a high pass amplitude filter for GFP, since it is produced when the AHL levels are sufficiently high. <br><br> </p> | |
| - | + | ||
| - | + | The system of equations for the states involved in the receiver colonies are given below: | |
| - | + | \begin{align} | |
| + | \frac{d[LuxR]}{dt}=\alpha_{LuxR} - d_{LuxR} \cdot [LuxR] \\ | ||
| + | \end{align} | ||
| - | + | \begin{align} | |
| + | \frac{d[R]}{dt}=\rho_{LuxR} \cdot [LuxR]^2 \cdot [AHL]^2 - d_{R} \cdot [R] \\ | ||
| + | \end{align} | ||
| - | + | \begin{align} | |
| + | \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} [AHL] - DF \cdot (d_{AHL,i} \cdot [AHL]) \\ | ||
| + | \end{align} | ||
| - | [[ | + | \begin{align} |
| + | \frac{d[GFP]}{dt}=\alpha_{GFP} \cdot k_{GFP} \cdot [LuxR] + \frac{\alpha_{GFP}\left(\frac{[R]}{K_{R}}\right)^{n}}{1+\left(\frac{[R]}{K_{R}}\right)^{n}} - d_{GFP}\cdot [GFP]\\ | ||
| + | \end{align} | ||
| + | <p align="center">System of Differential equations for receiver colonies.</p> | ||
| + | |||
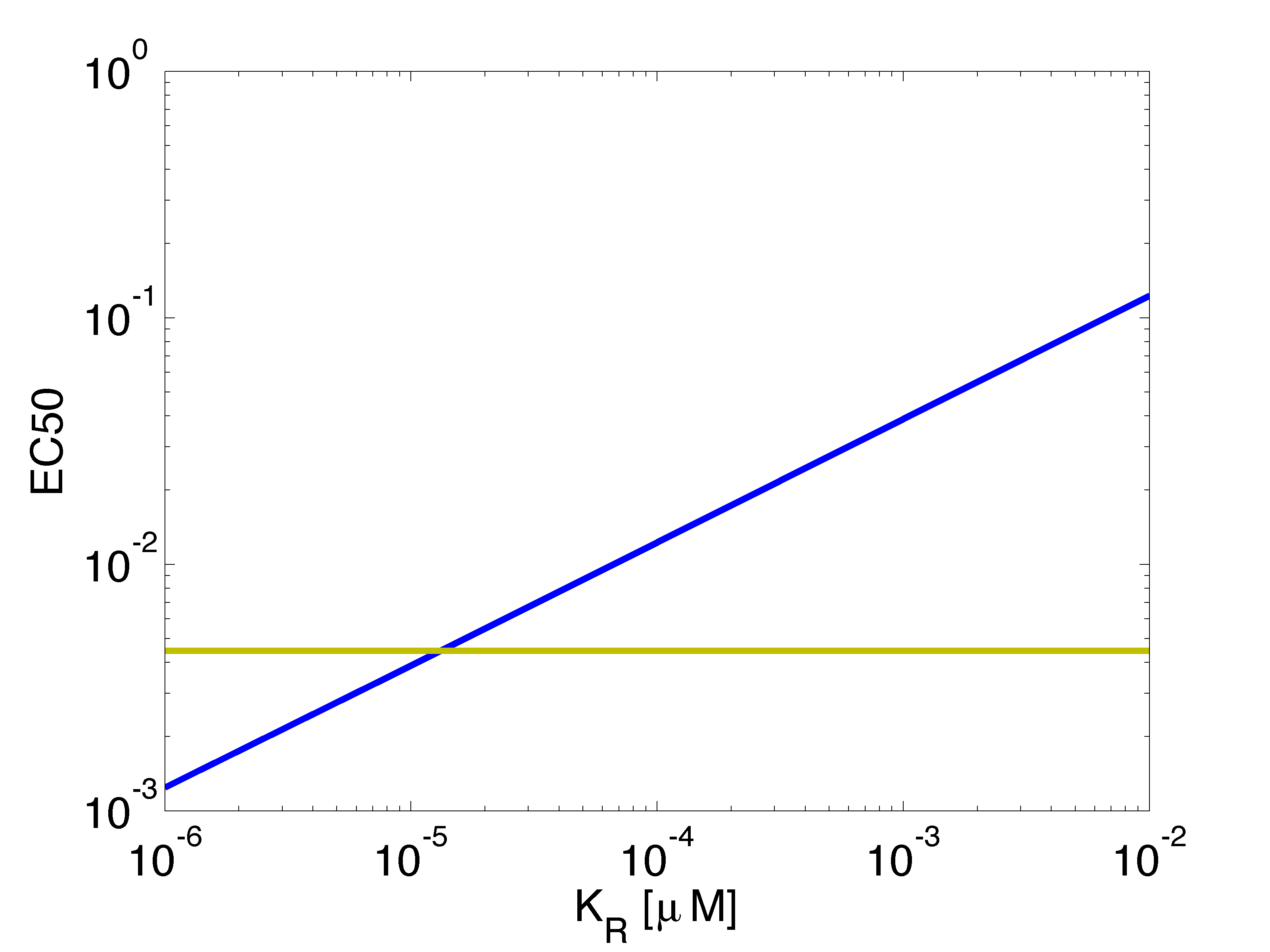
| + | <p align="justify"> The parameters used for the simulation correspond to values reported in literature and some of them were obtained from our experiments, like the growth rate and the affinity constant of the dimer LuxR/AHL. Also, simulations were initialised using [https://2013.igem.org/Team:ETH_Zurich/Modeling/InitialStates steady state concentrations] from single cell model for sender and receiver cells. Particularly, $K_{R}$ was derived using the promoter affinity obtained from experimental data (Fig. 1, [https://2013.igem.org/Team:ETH_Zurich/Experiments_5 EC<sub>50</sub> wild type]). The EC<sub>50</sub> value was obtained as function of AHL, but the model accounts for the LuxR/AHL complex. </p> <br> | ||
| + | |||
| + | [[File:KR EC50.png|500px|center|thumb|<b>Figure 1: </b> Estimated $K_{R}$.]] | ||
<h1>Results: Simulation</h1> | <h1>Results: Simulation</h1> | ||
| + | |||
| + | <p align="justify"> The goal of the simulation was to compare it to experimental results, thus it was conducted for 11 hours and with 3 mine cells to mimic the experimental setup (Figures 2-5). It can be seen that the predicted time scale for the expression of GFP from the simulation and the experimental results are congruent. In addition, it is very important to point out that: </p><br> | ||
| + | |||
| + | # The intensity of the GFP correlates with the number of adjacent mines, thus a suitable AHL gradient is formed. <br> | ||
| + | # The contribution from the basal expression cannot be neglected. <br><br> | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Gfp_5_5h.png|700px|center|thumb|<b>Figure 2: </b> Comparison between experimental, shown on the left, and simulation results, shown on the right, after 5.5 h. The experiments were performed in triplicates; Location of the mine cells: row 2 - third colony from left to right, row 3 - fifth colony from left to right, row 4 - fourth colony from left to right. ]] | ||
| + | [[File:Gfp_6_5h.png|700px|center|thumb|<b>Figure 3: </b> Comparison between experimental, shown on the left, and simulation results, shown on the right, after 6.5 h. The experiments were performed in triplicates; Location of the mine cells: row 2 - third colony from left to right, row 3 - fifth colony from left to right, row 4 - fourth colony from left to right. ]] | ||
| + | [[File:Gfp_9_5h.png|700px|center|thumb|<b>Figure 4: </b> Comparison between experimental, shown on the left, and simulation results, shown on the right, after 9.5 h. The experiments were performed in triplicates; Location of the mine cells: row 2 - third colony from left to right, row 3 - fifth colony from left to right, row 4 - fourth colony from left to right. ]] | ||
| + | [[File:Gfp_11h.png|700px|center|thumb|<b>Figure 5: </b> Comparison between experimental, shown on the left, and simulation results, shown on the right, after 11 h. The experiments were performed in triplicates; Location of the mine cells: row 2 - third colony from left to right, row 3 - fifth colony from left to right, row 4 - fourth colony from left to right.]] | ||
| + | <br> | ||
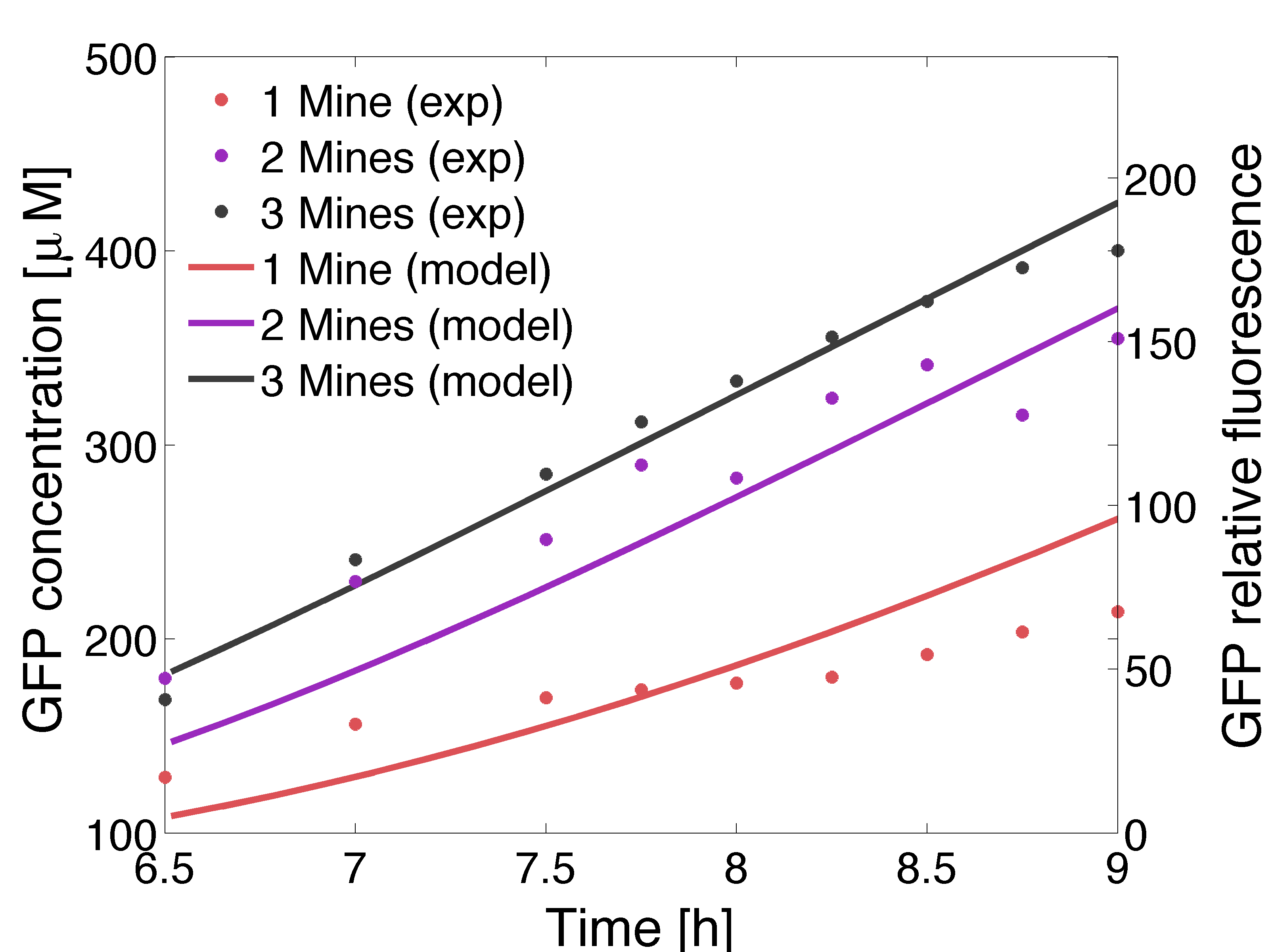
| + | <p align="justify"> From figures 2-5 we can conclude that experimental results and model predictions are in good agreement. Moreover, previous observations about activation by complex LuxR/AHL and time scales ([https://2013.igem.org/Team:ETH_Zurich/Modeling/Reaction_Diffusion_OOHL ''OHHL Reaction-Diffusion'']) are consistent with this findings. At 5.5 hours, there is non-differencial activation by LuxR/AHL complex which can be visualized as non-differential expression of GFP. At 6.5 hours, we start to see some differential expression of GFP related to the number of neighbouring mine colonies. Finally, after 11 hours, it is possible to clearly distinguish between 0, 1 and 2 neighbouring mines by GFP intensity. However, the difference in fluorescence in the case of 2 and 3 neighbouring mines, it is not significant. Hence, we decide to move to a three neighbours setup; removing the internal colony in the hexagonal grid and restrict to a maximum of 2 neighbouring mines. Based on figure 6, we can also confirmed that the experimental results and model predictions are consistent; we are showing the time points only for the exponential growth ([https://2013.igem.org/Team:ETH_Zurich/Modeling/Reaction_Diffusion_OOHL#growth view]). The experimental data was obtained by image analysis. </p> <br> | ||
| + | |||
| + | {|style="border: none; background: transparent;" align="center" | ||
| + | |valign="top" style="border:none;"|[[File:Gfp_pop.png|center|500px|thumb|<b>Figure 6: Experimental validation of the model </b> GFP fluorescence over time.]] | ||
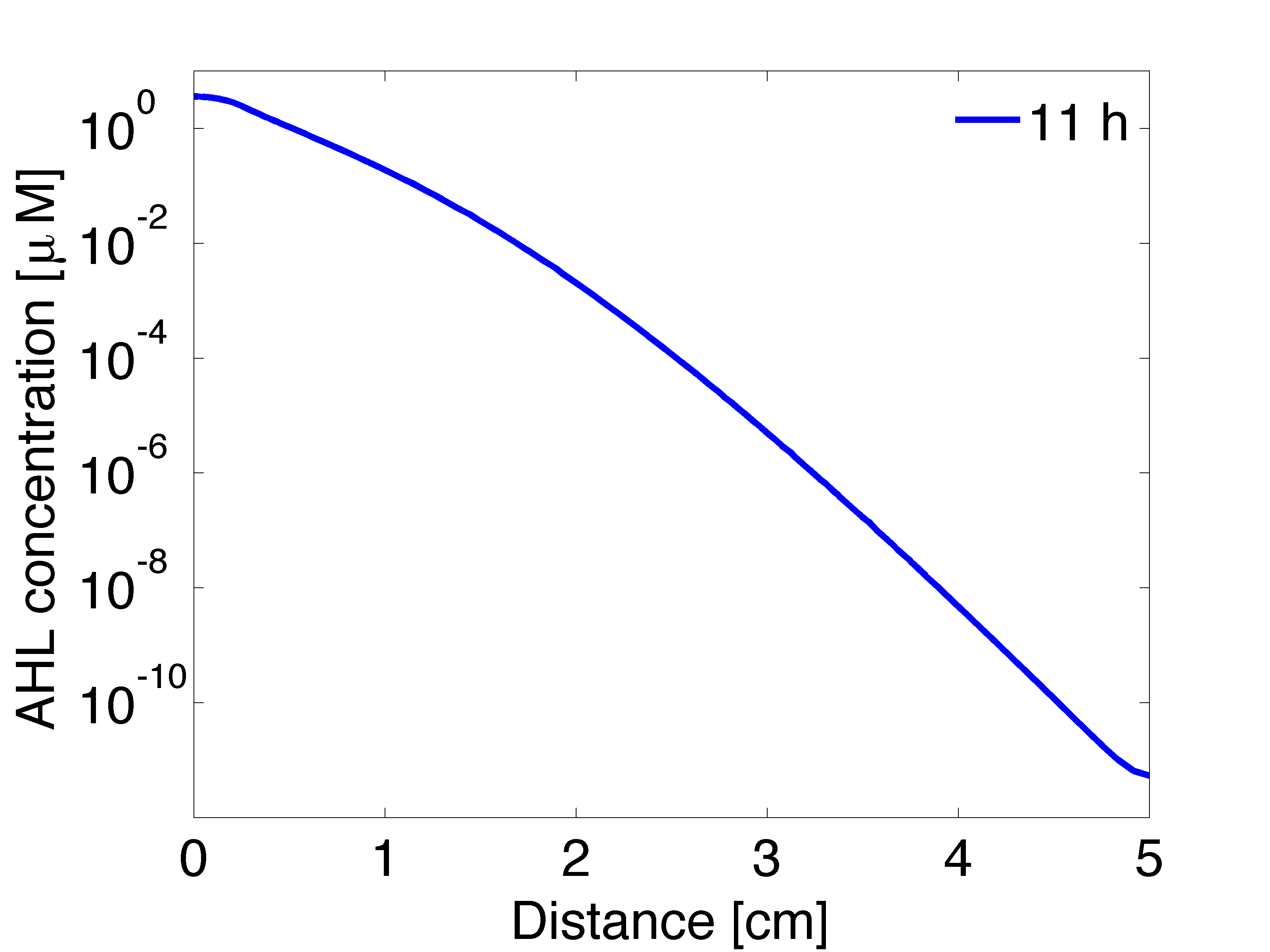
| + | |valign="top" style="border:none;"|[[File:AHL_11h.png|500px|center|thumb|<b>Figure 7: AHL concentration gradient established by a single mine colony </b> after 11 hours and radial direction, 2D model.]] | ||
| + | |} | ||
| + | |||
| + | <h1> Results: Model incorporating AHL inhibition </h1> | ||
| + | |||
| + | <html><a id="AHLinh" class="frog"></a></html> | ||
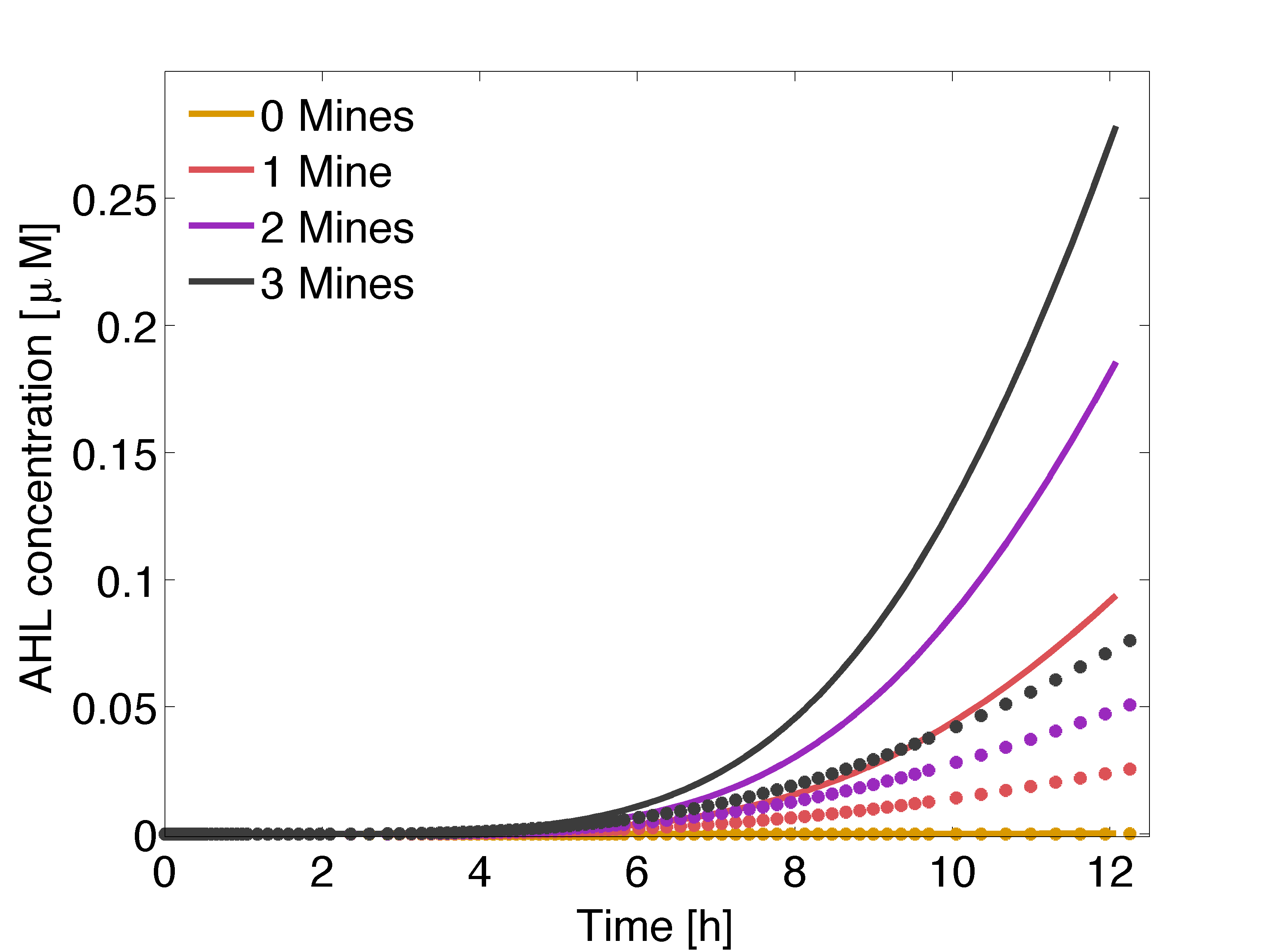
| + | <p align="justify"> From figures 8 and 9, we can conclude that although AHL gradient is significantly different, the output is robust. </p><br> | ||
| + | {|style="border: none; background: transparent;" align="center" | ||
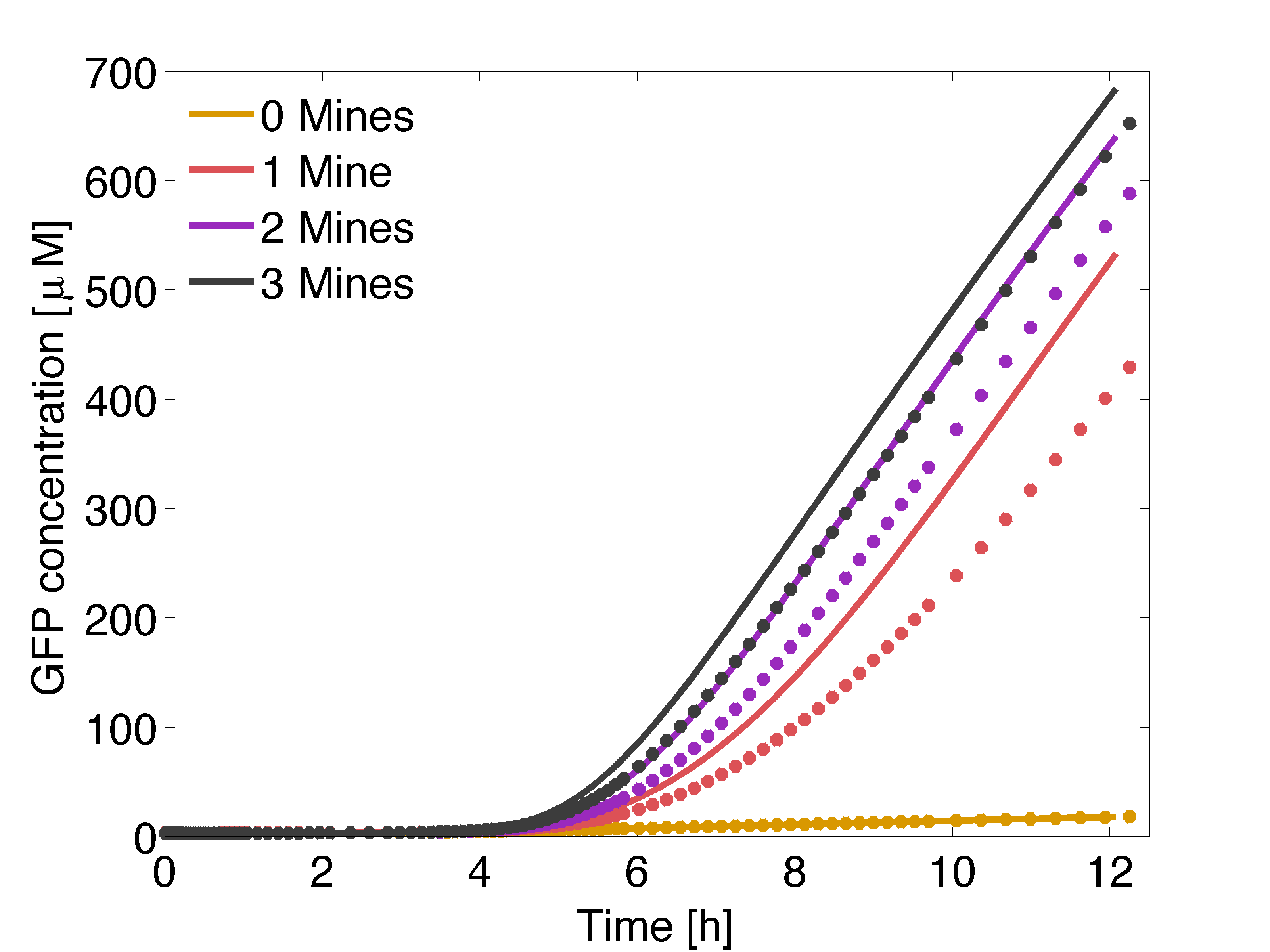
| + | |valign="top" style="border:none;"|[[File:AHLinh.png|center|500px|thumb|<b>Figure 8:</b> Averaged AHL concentration over time at receiver colonies with 0, 1, 2 or 3 neighbouring mine colonies, in μM. Distance between colonies: 1.5 cm. Dotes: Model with AHL inhibition $K_I = 1 \mu M$. Solid Lines: Model without AHL inhibition.]] | ||
| + | |valign="top" style="border:none;"|[[File:AHLinh GFP.png|500px|center|thumb|<b>Figure 9:</b> Averaged GFP concentration over time produced by a receiver colonies depending on number of neighbouring cell, in μM. Dotes: Model with AHL inhibition $K_I = 1 \mu M$. Solid Lines: Model without AHL inhibition.]] | ||
| + | |} | ||
<br clear="all"/> | <br clear="all"/> | ||
{{:Team:ETH_Zurich/templates/footer}} | {{:Team:ETH_Zurich/templates/footer}} | ||
Latest revision as of 10:42, 16 November 2013
Contents |
Reaction-diffusion model: genetic circuit with GFP as reporter gene
Building on our first spatio-temporal model for AHL, we wanted to evaluate the model with experimental data, as a proof of concept. In order to detect the diffusible molecule, we designed an experiment with receiver cells containing GFP under the control of PLuxR promoter (wild type). Subsequently, we simulate a 2D spatio-temporal reaction-diffusion system including GFP under control of PLuxR with COMSOL Multiphysics.
Video: GFP expression levels over 11 hours, concentration in mol/m3. Distance between colonies: 1,5 cm.
AHL diffuses in and out of mine cells, however the concentrations of species are time- and space-dependent. Thus the change of concentrations over time is given by system of non-linear partial differential equations (PDEs). Each equation represents the rate of change of species' continuous concentration as a sum of terms representing biological processes, such as production, degradation and regulation. The regulation is captured with Michaelis-Menten and Hill functions. For simplicity, we lump together specific cellular processes like transcription and translation, and do not model them explicitly.
Our system consists of two types of genetically engineered colonies: (i) Mine Cells and (ii) Receiver Cells, that can be treated as modules that communicate only by a single molecule, AHL. Additionally, we include the decay of AHL while diffusing through the agar plate.
Mine colony
One protein is produced by mine colonies, LuxI, which is constitutively expressed and linearly degraded. Additionally, the synthesis of AHL is carried on by these sender cells; the product of luxI gene is directly involved in the synthesis of the signalling molecule, using as substrates S-adenosylmethionine (SAM) and an acylated acyl carrier protein (ACP) from the fatty acid biosynthesis pathway (Schaefer et al., 1996). We assume precursor molecules are provided by the cell in non-limiting conditions.
The system of equations for the states involved in the sender module are given below:
\begin{align} \frac{d[LuxI]}{dt} = \alpha_{LuxI} - d_{LuxI} \cdot [LuxI]\\ \end{align}
\begin{align} \frac{d[AHL]}{dt} = DF \cdot ( \alpha_{AHL} \cdot [LuxI] - d_{AHL,i} \cdot [AHL] ) + C_{agar} \cdot D_{AHL} \nabla^{2} [AHL] \end{align}
System of Differential equations for mine colonies.
Agar plate
In the agar plate no reactions take place; hence only two processes of interested are considered: (i) diffusion and (ii) decay of the diffusible signal, AHL (Eq 6). The equation for AHL in agar plate is given below:
\begin{align} \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} [AHL] - d_{AHL,e} \cdot [AHL] \end{align}
Processes taking place on the agar plate: diffusion and decay of AHL.
Receiver colony
Receiver cells are responsible for processing the signal sent by the mine cells. AHL acts as the input signal and the output is green fluorescence whose intensity correlates with the sensed AHL concentration by receiver cells; for this purpose GFP expression is under the control of pLux promoter. Once AHL molecules reach a non-mine colony, they can bind to LuxR protein, and the complex LuxR/AHL acts as a transcriptional activator. Therefore, this module works as a high pass amplitude filter for GFP, since it is produced when the AHL levels are sufficiently high.
The system of equations for the states involved in the receiver colonies are given below:
\begin{align} \frac{d[LuxR]}{dt}=\alpha_{LuxR} - d_{LuxR} \cdot [LuxR] \\ \end{align}
\begin{align} \frac{d[R]}{dt}=\rho_{LuxR} \cdot [LuxR]^2 \cdot [AHL]^2 - d_{R} \cdot [R] \\ \end{align}
\begin{align} \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} [AHL] - DF \cdot (d_{AHL,i} \cdot [AHL]) \\ \end{align}
\begin{align} \frac{d[GFP]}{dt}=\alpha_{GFP} \cdot k_{GFP} \cdot [LuxR] + \frac{\alpha_{GFP}\left(\frac{[R]}{K_{R}}\right)^{n}}{1+\left(\frac{[R]}{K_{R}}\right)^{n}} - d_{GFP}\cdot [GFP]\\ \end{align}
System of Differential equations for receiver colonies.
The parameters used for the simulation correspond to values reported in literature and some of them were obtained from our experiments, like the growth rate and the affinity constant of the dimer LuxR/AHL. Also, simulations were initialised using steady state concentrations from single cell model for sender and receiver cells. Particularly, $K_{R}$ was derived using the promoter affinity obtained from experimental data (Fig. 1, EC50 wild type). The EC50 value was obtained as function of AHL, but the model accounts for the LuxR/AHL complex.
Results: Simulation
The goal of the simulation was to compare it to experimental results, thus it was conducted for 11 hours and with 3 mine cells to mimic the experimental setup (Figures 2-5). It can be seen that the predicted time scale for the expression of GFP from the simulation and the experimental results are congruent. In addition, it is very important to point out that:
- The intensity of the GFP correlates with the number of adjacent mines, thus a suitable AHL gradient is formed.
- The contribution from the basal expression cannot be neglected.




From figures 2-5 we can conclude that experimental results and model predictions are in good agreement. Moreover, previous observations about activation by complex LuxR/AHL and time scales (OHHL Reaction-Diffusion) are consistent with this findings. At 5.5 hours, there is non-differencial activation by LuxR/AHL complex which can be visualized as non-differential expression of GFP. At 6.5 hours, we start to see some differential expression of GFP related to the number of neighbouring mine colonies. Finally, after 11 hours, it is possible to clearly distinguish between 0, 1 and 2 neighbouring mines by GFP intensity. However, the difference in fluorescence in the case of 2 and 3 neighbouring mines, it is not significant. Hence, we decide to move to a three neighbours setup; removing the internal colony in the hexagonal grid and restrict to a maximum of 2 neighbouring mines. Based on figure 6, we can also confirmed that the experimental results and model predictions are consistent; we are showing the time points only for the exponential growth (view). The experimental data was obtained by image analysis.
Results: Model incorporating AHL inhibition
From figures 8 and 9, we can conclude that although AHL gradient is significantly different, the output is robust.
 "
"