Team:ETH Zurich/Modeling/Analytical Approximations
From 2013.igem.org
| (67 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
{{:Team:ETH_Zurich/Templates/stylesheet}} | {{:Team:ETH_Zurich/Templates/stylesheet}} | ||
| - | <h1>Steady State AHL Gradient Approximation</h1> | + | <h1><b>Steady State AHL Gradient Approximation</b></h1> |
<p align = "justify">In the reaction-diffusion model we have formalized the gradient establishment and we solved the resulting partial differential equation numerically. Now, the aim is to derive a suitable analytical approximation for a single mine colony. </p> | <p align = "justify">In the reaction-diffusion model we have formalized the gradient establishment and we solved the resulting partial differential equation numerically. Now, the aim is to derive a suitable analytical approximation for a single mine colony. </p> | ||
<h1> Kolmogorov-Petrovsky-Piskounov Equation </h1> | <h1> Kolmogorov-Petrovsky-Piskounov Equation </h1> | ||
| - | <p align = "justify"> | + | <p align = "justify">We consider the Kolmogorov-Petrovsky-Piskounov equation, i.e., the reaction–diffusion equation concerning the concentration of a single molecule. In our case we consider two spatial dimensions, and the equation for AHL then has the following general structure:</p><br> |
\begin{align} | \begin{align} | ||
| - | \frac{\partial AHL( | + | \frac{\partial AHL(r,\theta,t)}{\partial t} = Diff(AHL(r,\theta,t),r,\theta) + R(AHL(r,\theta,t)) |
\end{align} | \end{align} | ||
<br> | <br> | ||
| - | <p align = "justify"> We were interested in the AHL gradient that can be established by a single colony ( located at $ | + | <p align = "justify">We were interested in the AHL gradient that can be established by a single colony (located at $r = 0$ with radius $R = 2.5mm$) on an agar plate, ending up with a less general form of the reaction-diffusion model for AHL. The dependency on the angle $\theta$ can be disregarded the gradient established in two dimensions is radially symmetric. The polar coordinate Laplace operator for such a problem is</p> |
\begin{align} | \begin{align} | ||
| - | \ | + | \nabla^{2} f = \frac{1}{r} \frac{\partial f}{\partial r} + \frac{\partial^2 f}{\partial r^2} |
\end{align} | \end{align} | ||
| - | + | <p align="justify">The reaction-diffusion equation (Gordon ''et al.'', 2013) then reads</p> | |
| - | <p align = "justify"> | + | |
\begin{align} | \begin{align} | ||
| - | [AHL]( | + | \frac{\partial [AHL](r, t)}{\partial t} & = & C_{agar} \cdot D_{AHL} \nabla^{2} [AHL](r, t) - d_{AHL,e} \cdot [AHL](r, t) \\ |
| + | & = & C_{agar} \cdot D_{AHL} \left( \frac{1}{r} \frac{\partial [AHL](r, t)}{\partial r} + \frac{\partial^2 [AHL](r, t)}{\partial r^2}\right) - d_{AHL,e} \cdot [AHL] (r, t) | ||
\end{align} | \end{align} | ||
| + | with boundary conditions | ||
| + | |||
| + | \begin{align} | ||
| + | - D \frac{\partial [AHL]}{\partial r}(R, t) & = & Q \\ | ||
| + | [AHL](r, 0) & = & 0. | ||
| + | \end{align} | ||
| - | |||
<h1> Solution at the steady state </h1> | <h1> Solution at the steady state </h1> | ||
| - | + | The steady state solution is described by the differential equation | |
\begin{align} | \begin{align} | ||
| - | + | 0 & = & C_{agar} \cdot D_{AHL} \left(\frac{1}{r} \frac{\partial [AHL](r)}{\partial r} + \frac{\partial^2 [AHL](r)}{\partial r^2}\right) - d_{AHL,e} \cdot [AHL] (r) | |
\end{align} | \end{align} | ||
| + | |||
| + | with boundary conditions | ||
| + | |||
\begin{align} | \begin{align} | ||
| - | \frac{\partial | + | - D \frac{\partial [AHL]}{\partial r}(R) & = & Q \\ |
| + | [AHL](\infty) & = & 0. | ||
| + | \end{align} | ||
| + | |||
| + | The solution to this problem is (Gordon ''et al.'', 2013) described by the equation | ||
| + | |||
| + | \begin{align} | ||
| + | [AHL](r) = \frac{Q}{\sqrt{ C_{agar} D_{AHL} d_{AHL,e} }} \frac{K_0(\sqrt{d_{AHL,e}} r / \sqrt{C_{agar} D_{AHL}})}{K_1(\sqrt{d_{AHL,e}} R / \sqrt{C_{agar} D_{AHL}})} | ||
| + | \end{align} | ||
| + | |||
| + | where $r >= R$ and $K_0(r), K_1(r)$ are modified Bessel functions of the second kind. | ||
| + | |||
| + | We now need to calculate the outflux of AHL from the mine colony, i.e., $Q$, for our system. This can be done by setting the concentration of AHL at $r = R$, i.e., $[AHL](R)$, to the steady state of the mine cells calculated including the AHL outflow Q. The steady state, including outflow, in the mine colony is given by the equation | ||
| + | |||
| + | \begin{align} | ||
| + | 0 & = & \alpha_{AHL} \frac{\alpha_{LuxI}}{d_{LuxI}} - d_{AHL,i}[AHL] - Q \frac{2}{R}. | ||
| + | \end{align} | ||
| + | |||
| + | Solving both equations $(10)$ and $(11)$ with respect to $[AHL]$ and setting them equal gives the result | ||
| + | \begin{align} | ||
| + | Q = \frac{\alpha_{AHL} \frac{\alpha_{LuxI}}{d_{LuxI}} R}{R \cdot S \cdot d_{AHL,i} + 2} | ||
| + | \end{align} | ||
| + | |||
| + | with | ||
| + | |||
| + | \begin{align} | ||
| + | S = \frac{1}{\sqrt{C_{agar} D_{AHL} d_{AHL,e}}} \frac{K_0(\sqrt{d_{AHL,e}} R / \sqrt{C_{agar} D_{AHL}})}{K_1(\sqrt{d_{AHL,e}} R / \sqrt{C_{agar} D_{AHL}})}. | ||
\end{align} | \end{align} | ||
<br> | <br> | ||
| - | <p align = " | + | <p align = "center"><b> Comparison with numerical solution </b></p> |
| + | We can now evaluate the analytical result obtained with the exact numerical result to determine if the gradient is accurately estimated. Figure 1 clearly shows the accuracy of the obtained result for $r >= R$, whereas for $r < R$ we assume a constant concentration inside the mine colony. This is obviously not the case, however, for the purpose of evaluating the gradient at the receiver cells at $r = 1.5cm$, we deem the accuracy of the result to be sufficient. | ||
| + | <br> | ||
| + | <br> | ||
| + | |||
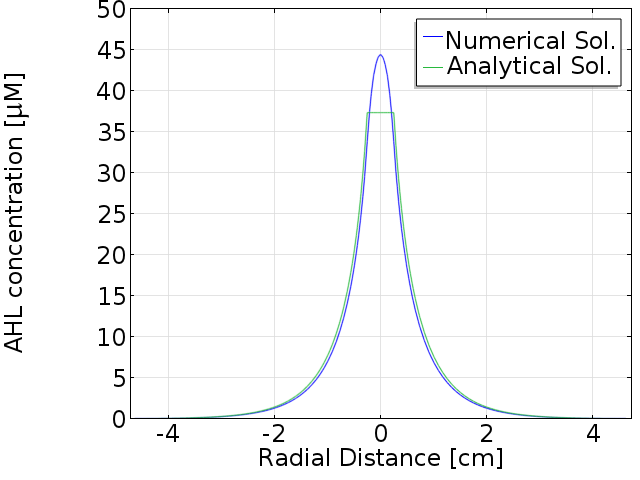
| + | [[File:AHLss analytical.png|600px|center|thumb|<b>Figure 1:</b> Analytical approximation and numerical solution of the AHL gradient. Note that for $r < R$ the derived formula cannot be used, therefore a straight line was plotted.]] | ||
| + | |||
| + | |||
| + | <h1> <b>Search for an optimal promoter mutant </b></h1> | ||
| + | |||
| + | <p align = "justify">For the case of 2 neighbouring mines, we need to introduce a second promoter with a different sensitivity towards the complex LuxR/AHL. Experimentally the problem was addressed by constructing a library of promoter mutants. From the model we wanted to evaluate the mutants in order to predict which one could be the best. </p> | ||
| + | |||
| + | <p align = "justify">In order to reduce the calculations, the current model with 6 species can be simplified to 3 species. Basically, proteins that are constitutively produced and linearly degraded can be assumed to be constants, which is the case for LuxI and LuxR, that are set to the steady state concentration. Regarding the complex LuxR/AHL, we can express production of the output proteins controlled by AHL. Thus, we have senders cells producing AHL and receiver cells processing the signal and giving colour outputs depending on the number of neighbouring mines. </p> | ||
| + | <br> | ||
| + | |||
| + | <b>Mine Colony</b> | ||
\begin{align} | \begin{align} | ||
| - | [AHL] | + | \frac{d[AHL]}{dt} = DF \cdot ( \alpha_{AHL} \cdot [LuxI] - d_{AHL,i} \cdot [AHL] ) + C_{agar} \cdot D_{AHL} \nabla^{2} AHL |
\end{align} | \end{align} | ||
| - | [[File: | + | <b>Agar Plate </b> |
| + | |||
| + | \begin{align} | ||
| + | \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} AHL-d_{AHL,e} \cdot [AHL] | ||
| + | \end{align} | ||
| + | |||
| + | <b> Receiver Colony </b> | ||
| + | |||
| + | \begin{align} | ||
| + | \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} AHL - DF \cdot \left(d_{AHL,i} \cdot [AHL]\right) \\ | ||
| + | \end{align} | ||
| + | |||
| + | \begin{align} | ||
| + | \frac{d[E_{1}]}{dt}=\alpha_{E_{1}} \cdot k_{basal} \cdot [LuxR]_{ss} + \frac{\alpha_{E_{1}}\left(\frac{[AHL]}{K_{M_{ wt}}}\right)^{2}}{1+\left(\frac{[AHL]}{K_{M_{ wt}}}\right)^{2}} - d_{E_{1}}\cdot [E_{1}]\\ | ||
| + | \end{align} | ||
| + | |||
| + | \begin{align} | ||
| + | \frac{d[E_{2}]}{dt}=\alpha_{E_{2}} \cdot k_{basal} \cdot [LuxR]_{ss} + \frac{\alpha_{E_{2}}\left(\frac{[AHL]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL]}{K_{M_{ mut}}}\right)^{2}} - d_{E_{2}}\cdot [E_{2}]\\ | ||
| + | \end{align} | ||
| + | |||
| + | <p align = "justify"> $E_{1}$ an $E_{2}$ is a abstract way to indicate the output system for the case of 1 or 2 neighbouring mines. The output system can consist either of fluorescent proteins, GFP and RFP, or hydrolases, GusA and AES. </p> | ||
| + | |||
| + | <p align = "justify"> The second protein, $E_{2}$, is responsible to give a colour output that indicate the presence of two mines. Its synthesis should start with some delayed after the first protein, given that the promoter is less sensitive to AHL. However, this protein is also expressed by colonies surrounded by a single mine colony. Our goal is to ensure that the ratio of expression levels for 2 to 1 neighbouring mines is large enough. Taking the limit for this ratio we got:</p> | ||
| + | |||
| + | \begin{align} | ||
| + | \lim_{K_{M_{ mut}} \to \infty} | ||
| + | \frac{\left(\frac{[AHL_{2}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{2}]}{K_{M_{ mut}}}\right)^{2}} \Bigg / | ||
| + | \frac{\left(\frac{[AHL_{1}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{1}]}{K_{M_{ mut}}}\right)^{2}} = \lim_{K_{M_{ mut}} \to \infty} \left(\frac{[AHL_{2}]}{[AHL_{1}]} \right)^2 \frac{K_{M_{ mut}}^2 + [AHL_{1}]^2}{K_{M_{ mut}}^2 + [AHL_{2}]^2} = \left(\frac{[AHL_{2}]}{[AHL_{1}]} \right)^2 | ||
| + | \end{align} | ||
| + | |||
| + | <p align = "justify"> From the AHL [https://2013.igem.org/Team:ETH_Zurich/Modeling/Reaction_Diffusion_OOHL#2fold diffusion-reaction model], we learnt that as the number of neighboring mine colonies increases there is a two fold increment on AHL concentration at the receiver colonies; roughly $[AHL_{ 2}] = 2 \cdot [AHL_{ 1}]$. Thus, the best we can hope for is to obtain a ratio of 4. </p> | ||
| + | |||
| + | |||
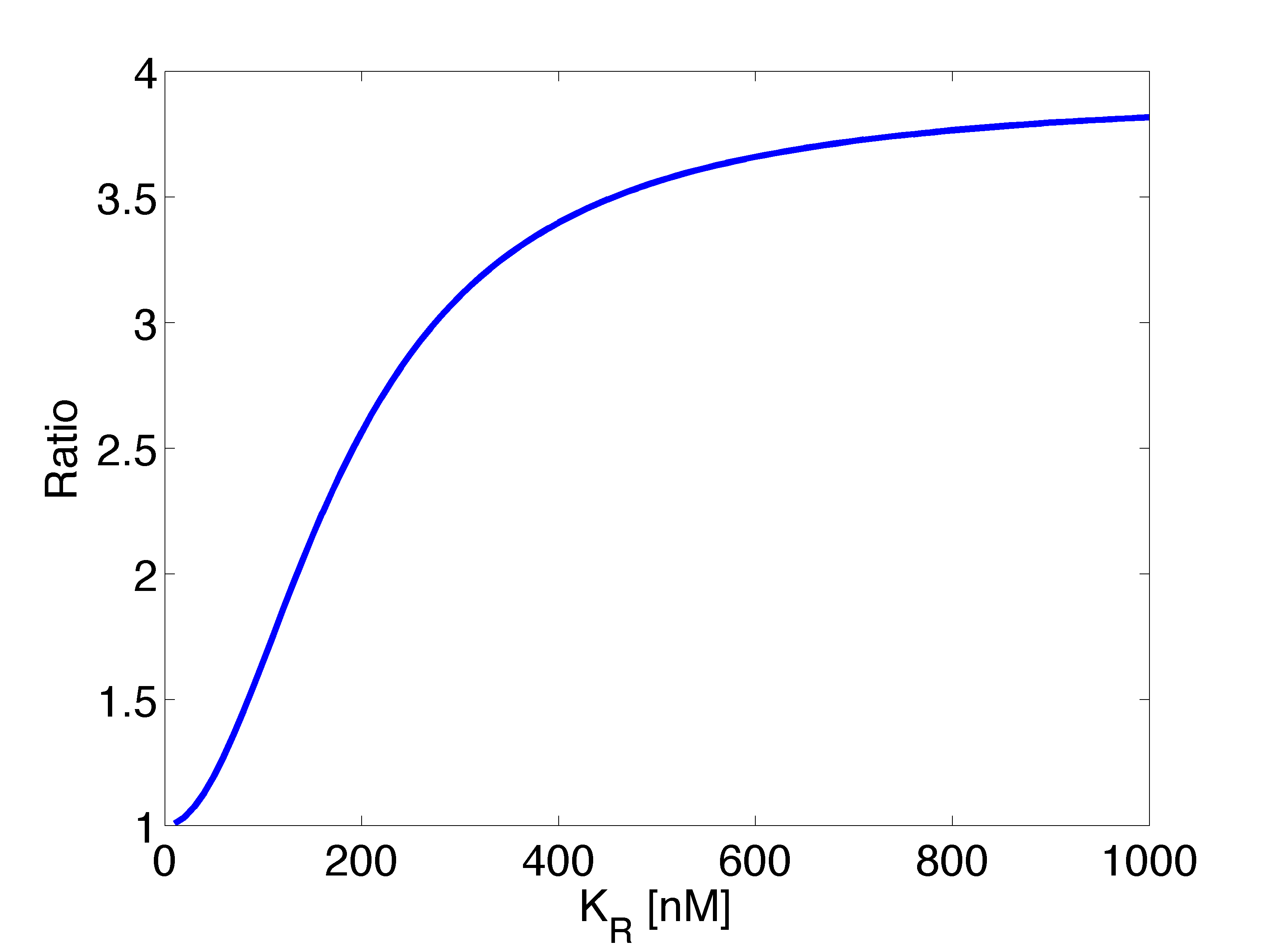
| + | [[File:KRratio.png|500px|center|thumb|<b>Figure 2: </b> Ratio in expression levels as function of $K_{R}$, using AHL concentration at receiver colonies surrounded by 1 and 2 mines after 11 hours and with 1.5 cm as distance between colonies. $[AHL_{1}] = 0.0938$ and $[AHL_{2}] = 0.1856$.]] | ||
| + | |||
| + | |||
| + | <p align="center"><b> [https://2013.igem.org/Team:ETH_Zurich/Experiments_5#promLibrary Promoter mutants] evaluation </b></p> | ||
| + | [[File:Promoter2.png|500px|center|thumb|<b>Figure 3: </b> Ratio in expression levels over time for promoter mutants.]] | ||
| + | <p align="center"> Protein concentration was obtained from the reduced model described above. </p> | ||
<br clear="all"/> | <br clear="all"/> | ||
| + | |||
| + | <p align = "justify"> We are still interested in determining the optimal $K_{M_{ mut}}$. For this purpose, we can maximize the difference between the regulation terms for 2 and 1 neighbouring mines: </p> | ||
| + | |||
| + | \begin{align} | ||
| + | \operatorname*{max}_{K_{M_{ mut}}} \frac{\left(\frac{[AHL_{ 2}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{2}]}{K_{M_{ mut}}}\right)^{2}} - \frac{\left(\frac{[AHL_{ 1}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{ 1}]}{K_{M_{ mut}}}\right)^{2}} | ||
| + | \end{align} | ||
| + | |||
| + | <p align = "justify"> Deriving equation 13 w.r.t. $K_{M_{ mut}}$ and set it to zero, we can obtain the following: </p> | ||
| + | |||
| + | \begin{align} | ||
| + | \frac{[AHL_{1}]^{2} \cdot K_{M_{ mut}}}{K_{M_{ mut}}^{2} + [AHL_{1}]^{2}} - | ||
| + | \frac{[AHL_{2}]^{2} \cdot K_{M_{ mut}}}{K_{M_{ mut}}^{2} + [AHL_{2}]^{2}} = 0 | ||
| + | \end{align} | ||
| + | |||
| + | \begin{align} | ||
| + | K_{M_{ mut}} = \sqrt[4]{ | ||
| + | \frac | ||
| + | {[AHL_{1}]^{2} \cdot [AHL_{2}]^{4} - [AHL_{1}]^{4} \cdot [AHL_{2}]^{2} } | ||
| + | {[AHL_{2}]^{2}-[AHL_{1}]^{2}} | ||
| + | } | ||
| + | \end{align} | ||
| + | |||
| + | <p align = "justify"> Once again, considering that $[AHL_{ 2}] = 2 \cdot [AHL_{ 1}]$, we have: </p> | ||
| + | |||
| + | \begin{align} | ||
| + | K_{M_{ mut}} = \sqrt{2} \cdot [AHL_{1}] | ||
| + | \end{align} | ||
| + | |||
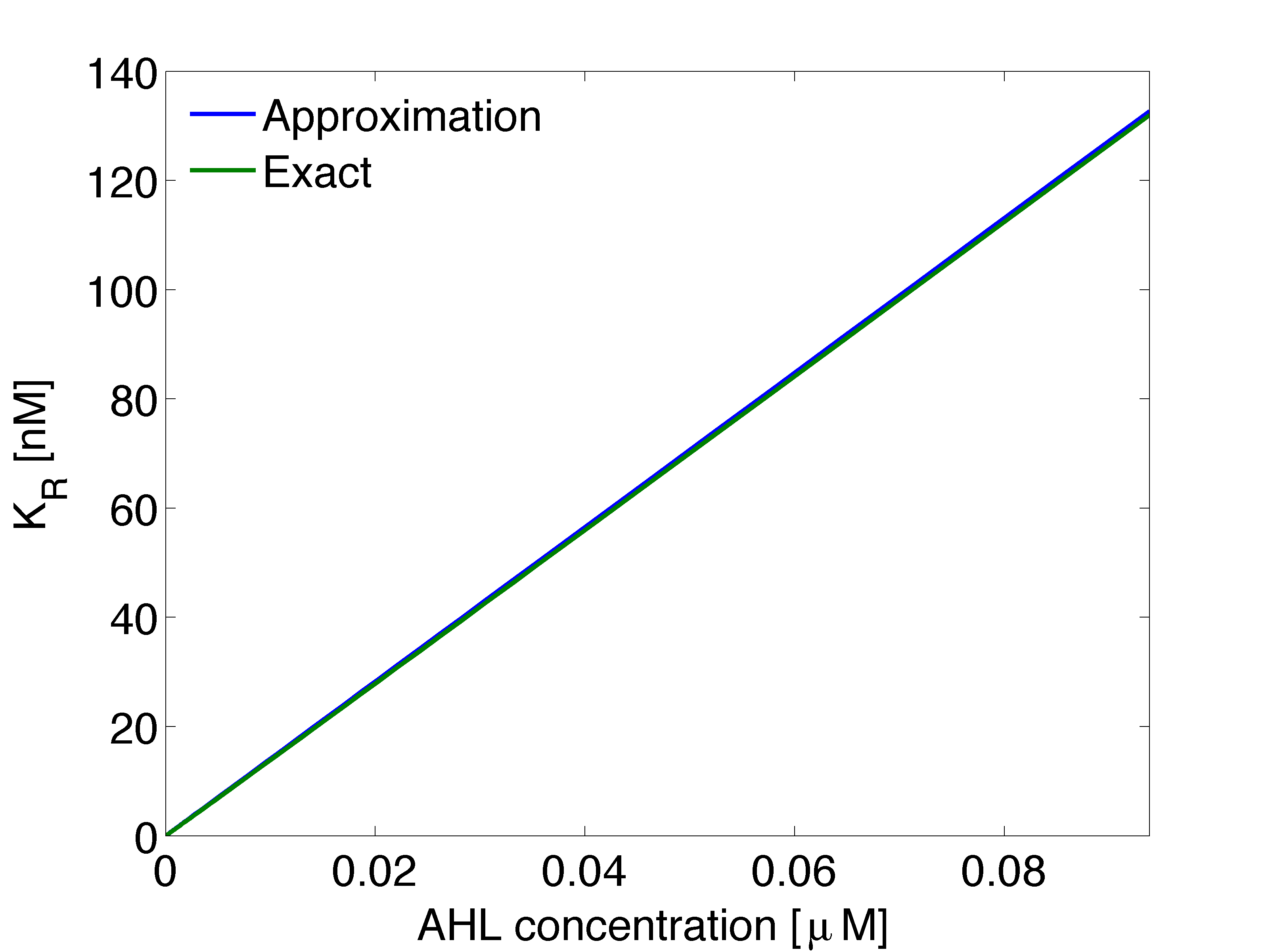
| + | [[File:KRahl.png|500px|center|thumb|<b>Figure 4: </b> Optimal $K_{R}$ as function of AHL concentration at receiver colonies surrounded by 1 mine. Exact: computed from equation 15. Approximation: computed from equation 16. ]] | ||
| + | <br> | ||
{{:Team:ETH_Zurich/templates/footer}} | {{:Team:ETH_Zurich/templates/footer}} | ||
Latest revision as of 20:06, 15 November 2013
Contents |
Steady State AHL Gradient Approximation
In the reaction-diffusion model we have formalized the gradient establishment and we solved the resulting partial differential equation numerically. Now, the aim is to derive a suitable analytical approximation for a single mine colony.
Kolmogorov-Petrovsky-Piskounov Equation
We consider the Kolmogorov-Petrovsky-Piskounov equation, i.e., the reaction–diffusion equation concerning the concentration of a single molecule. In our case we consider two spatial dimensions, and the equation for AHL then has the following general structure:
\begin{align} \frac{\partial AHL(r,\theta,t)}{\partial t} = Diff(AHL(r,\theta,t),r,\theta) + R(AHL(r,\theta,t)) \end{align}
We were interested in the AHL gradient that can be established by a single colony (located at $r = 0$ with radius $R = 2.5mm$) on an agar plate, ending up with a less general form of the reaction-diffusion model for AHL. The dependency on the angle $\theta$ can be disregarded the gradient established in two dimensions is radially symmetric. The polar coordinate Laplace operator for such a problem is
\begin{align} \nabla^{2} f = \frac{1}{r} \frac{\partial f}{\partial r} + \frac{\partial^2 f}{\partial r^2} \end{align}
The reaction-diffusion equation (Gordon et al., 2013) then reads
\begin{align} \frac{\partial [AHL](r, t)}{\partial t} & = & C_{agar} \cdot D_{AHL} \nabla^{2} [AHL](r, t) - d_{AHL,e} \cdot [AHL](r, t) \\ & = & C_{agar} \cdot D_{AHL} \left( \frac{1}{r} \frac{\partial [AHL](r, t)}{\partial r} + \frac{\partial^2 [AHL](r, t)}{\partial r^2}\right) - d_{AHL,e} \cdot [AHL] (r, t) \end{align}
with boundary conditions
\begin{align} - D \frac{\partial [AHL]}{\partial r}(R, t) & = & Q \\ [AHL](r, 0) & = & 0. \end{align}
Solution at the steady state
The steady state solution is described by the differential equation
\begin{align} 0 & = & C_{agar} \cdot D_{AHL} \left(\frac{1}{r} \frac{\partial [AHL](r)}{\partial r} + \frac{\partial^2 [AHL](r)}{\partial r^2}\right) - d_{AHL,e} \cdot [AHL] (r) \end{align}
with boundary conditions
\begin{align} - D \frac{\partial [AHL]}{\partial r}(R) & = & Q \\ [AHL](\infty) & = & 0. \end{align}
The solution to this problem is (Gordon et al., 2013) described by the equation
\begin{align} [AHL](r) = \frac{Q}{\sqrt{ C_{agar} D_{AHL} d_{AHL,e} }} \frac{K_0(\sqrt{d_{AHL,e}} r / \sqrt{C_{agar} D_{AHL}})}{K_1(\sqrt{d_{AHL,e}} R / \sqrt{C_{agar} D_{AHL}})} \end{align}
where $r >= R$ and $K_0(r), K_1(r)$ are modified Bessel functions of the second kind.
We now need to calculate the outflux of AHL from the mine colony, i.e., $Q$, for our system. This can be done by setting the concentration of AHL at $r = R$, i.e., $[AHL](R)$, to the steady state of the mine cells calculated including the AHL outflow Q. The steady state, including outflow, in the mine colony is given by the equation
\begin{align} 0 & = & \alpha_{AHL} \frac{\alpha_{LuxI}}{d_{LuxI}} - d_{AHL,i}[AHL] - Q \frac{2}{R}. \end{align}
Solving both equations $(10)$ and $(11)$ with respect to $[AHL]$ and setting them equal gives the result \begin{align} Q = \frac{\alpha_{AHL} \frac{\alpha_{LuxI}}{d_{LuxI}} R}{R \cdot S \cdot d_{AHL,i} + 2} \end{align}
with
\begin{align} S = \frac{1}{\sqrt{C_{agar} D_{AHL} d_{AHL,e}}} \frac{K_0(\sqrt{d_{AHL,e}} R / \sqrt{C_{agar} D_{AHL}})}{K_1(\sqrt{d_{AHL,e}} R / \sqrt{C_{agar} D_{AHL}})}. \end{align}
Comparison with numerical solution
We can now evaluate the analytical result obtained with the exact numerical result to determine if the gradient is accurately estimated. Figure 1 clearly shows the accuracy of the obtained result for $r >= R$, whereas for $r < R$ we assume a constant concentration inside the mine colony. This is obviously not the case, however, for the purpose of evaluating the gradient at the receiver cells at $r = 1.5cm$, we deem the accuracy of the result to be sufficient.
Search for an optimal promoter mutant
For the case of 2 neighbouring mines, we need to introduce a second promoter with a different sensitivity towards the complex LuxR/AHL. Experimentally the problem was addressed by constructing a library of promoter mutants. From the model we wanted to evaluate the mutants in order to predict which one could be the best.
In order to reduce the calculations, the current model with 6 species can be simplified to 3 species. Basically, proteins that are constitutively produced and linearly degraded can be assumed to be constants, which is the case for LuxI and LuxR, that are set to the steady state concentration. Regarding the complex LuxR/AHL, we can express production of the output proteins controlled by AHL. Thus, we have senders cells producing AHL and receiver cells processing the signal and giving colour outputs depending on the number of neighbouring mines.
Mine Colony
\begin{align} \frac{d[AHL]}{dt} = DF \cdot ( \alpha_{AHL} \cdot [LuxI] - d_{AHL,i} \cdot [AHL] ) + C_{agar} \cdot D_{AHL} \nabla^{2} AHL \end{align}
Agar Plate
\begin{align} \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} AHL-d_{AHL,e} \cdot [AHL] \end{align}
Receiver Colony
\begin{align} \frac{d[AHL]}{dt}= C_{agar} \cdot D_{AHL} \nabla^{2} AHL - DF \cdot \left(d_{AHL,i} \cdot [AHL]\right) \\ \end{align}
\begin{align} \frac{d[E_{1}]}{dt}=\alpha_{E_{1}} \cdot k_{basal} \cdot [LuxR]_{ss} + \frac{\alpha_{E_{1}}\left(\frac{[AHL]}{K_{M_{ wt}}}\right)^{2}}{1+\left(\frac{[AHL]}{K_{M_{ wt}}}\right)^{2}} - d_{E_{1}}\cdot [E_{1}]\\ \end{align}
\begin{align} \frac{d[E_{2}]}{dt}=\alpha_{E_{2}} \cdot k_{basal} \cdot [LuxR]_{ss} + \frac{\alpha_{E_{2}}\left(\frac{[AHL]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL]}{K_{M_{ mut}}}\right)^{2}} - d_{E_{2}}\cdot [E_{2}]\\ \end{align}
$E_{1}$ an $E_{2}$ is a abstract way to indicate the output system for the case of 1 or 2 neighbouring mines. The output system can consist either of fluorescent proteins, GFP and RFP, or hydrolases, GusA and AES.
The second protein, $E_{2}$, is responsible to give a colour output that indicate the presence of two mines. Its synthesis should start with some delayed after the first protein, given that the promoter is less sensitive to AHL. However, this protein is also expressed by colonies surrounded by a single mine colony. Our goal is to ensure that the ratio of expression levels for 2 to 1 neighbouring mines is large enough. Taking the limit for this ratio we got:
\begin{align} \lim_{K_{M_{ mut}} \to \infty} \frac{\left(\frac{[AHL_{2}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{2}]}{K_{M_{ mut}}}\right)^{2}} \Bigg / \frac{\left(\frac{[AHL_{1}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{1}]}{K_{M_{ mut}}}\right)^{2}} = \lim_{K_{M_{ mut}} \to \infty} \left(\frac{[AHL_{2}]}{[AHL_{1}]} \right)^2 \frac{K_{M_{ mut}}^2 + [AHL_{1}]^2}{K_{M_{ mut}}^2 + [AHL_{2}]^2} = \left(\frac{[AHL_{2}]}{[AHL_{1}]} \right)^2 \end{align}
From the AHL diffusion-reaction model, we learnt that as the number of neighboring mine colonies increases there is a two fold increment on AHL concentration at the receiver colonies; roughly $[AHL_{ 2}] = 2 \cdot [AHL_{ 1}]$. Thus, the best we can hope for is to obtain a ratio of 4.
Promoter mutants evaluation
Protein concentration was obtained from the reduced model described above.
We are still interested in determining the optimal $K_{M_{ mut}}$. For this purpose, we can maximize the difference between the regulation terms for 2 and 1 neighbouring mines:
\begin{align} \operatorname*{max}_{K_{M_{ mut}}} \frac{\left(\frac{[AHL_{ 2}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{2}]}{K_{M_{ mut}}}\right)^{2}} - \frac{\left(\frac{[AHL_{ 1}]}{K_{M_{ mut}}}\right)^{2}}{1+\left(\frac{[AHL_{ 1}]}{K_{M_{ mut}}}\right)^{2}} \end{align}
Deriving equation 13 w.r.t. $K_{M_{ mut}}$ and set it to zero, we can obtain the following:
\begin{align} \frac{[AHL_{1}]^{2} \cdot K_{M_{ mut}}}{K_{M_{ mut}}^{2} + [AHL_{1}]^{2}} - \frac{[AHL_{2}]^{2} \cdot K_{M_{ mut}}}{K_{M_{ mut}}^{2} + [AHL_{2}]^{2}} = 0 \end{align}
\begin{align} K_{M_{ mut}} = \sqrt[4]{ \frac {[AHL_{1}]^{2} \cdot [AHL_{2}]^{4} - [AHL_{1}]^{4} \cdot [AHL_{2}]^{2} } {[AHL_{2}]^{2}-[AHL_{1}]^{2}} } \end{align}
Once again, considering that $[AHL_{ 2}] = 2 \cdot [AHL_{ 1}]$, we have:
\begin{align} K_{M_{ mut}} = \sqrt{2} \cdot [AHL_{1}] \end{align}
 "
"