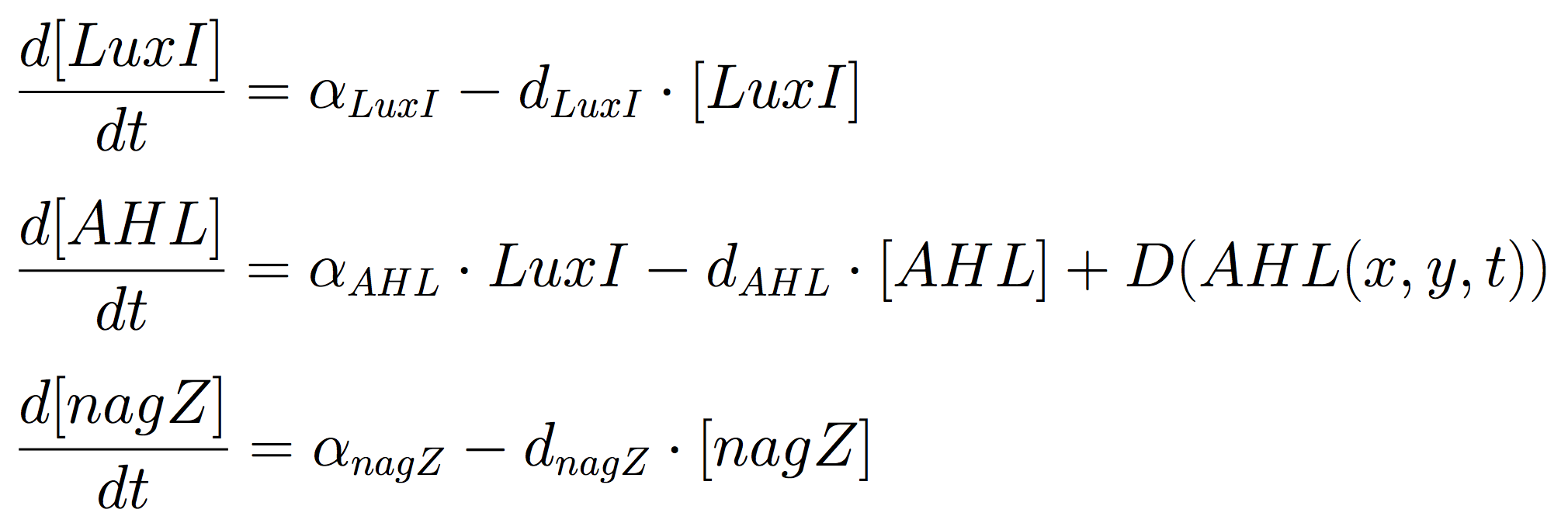The digital bacterial-based minesweeper

We created a two dimensional spatio-temporal model of the Colisweeper bacterial game in order to evaluate our network and design. For the simulation, we used the software COMSOL Multiphysics.

Figure 1: General partial differential equation for AHL reaction-diffusion. D(AHL(r,t),r) is the diffusive term, R(AHL(r,t)) is the reaction term

To explain how the concentration of AHL changes over time, we have to consider the influence of two processes: local chemical reactions and diffusion which causes the molecule to spread out over the agar plate (Fig. 1).

Figure 2: Diffusive term for AHL

For the Diffusion, the equation is a partial differential equation (Fig. 2) which describes density fluctuations over time and space. D_AHL(AHL(r,t),r) denotes the collective diffusion coefficient for AHL at location r. However, we are assuming that the diffusion coefficient does not depend on the density, i.e., D_AHL is a constant. The value reported in the literature for the diffusion constant corresponds to measurements performed in water at 25^oC. Since diffusion in our system happens in agar, we scaled the diffusion constant by a factor C_agar (Fatin-Rouge et al., 2004).

The change of the species concentrations in time is given by non-linear ordinary differential equations (ODEs), most of which follow Hill kinetics. The parameters we used in the model are derived from literature. In our model we consider that signalling molecules degrade at the same rate whether they are cytoplasmic or not.

Mine Cells

Figure 3: Differential equations of the mine cells

The Mine Cells lead to the synthesis the signalling molecule, by constitutive expression of luxI gene. To reveal the nature of the cells, a coloured-substrate reaction is triggered upon addition of 5-Bromo-4-chloro-3-indoxyl-N-acetyl-beta-D-glucosaminide; given that the glycoside hydrolase NagZ is expressed constitutively.

The ODEs for the states involved in the sender module are given below:

Receiver Cells

Figure 4: Differential equations of the receiver cells

Our Receiver cells are engineered to respond differently to high and medium concentrations of AHL. This cells are capable of discriminate between the presence of 1 or 2 mine cells around them in the immediate vicinity. To accomplish this task, the enzymes involved in the coloured-substrate reaction are sensitive to different concentrations of the dimer LuxR-AHL (denoted as R).