Team:ETH Zurich/Modeling/Analytical Approximations
From 2013.igem.org
| Line 45: | Line 45: | ||
[AHL] = [AHL]_{MineCell,ss} \cdot e^{-\sqrt{\frac{d_{AHL,e}} {C_{agar} \cdot D_{AHL}}} \cdot x} | [AHL] = [AHL]_{MineCell,ss} \cdot e^{-\sqrt{\frac{d_{AHL,e}} {C_{agar} \cdot D_{AHL}}} \cdot x} | ||
\end{align} | \end{align} | ||
| + | |||
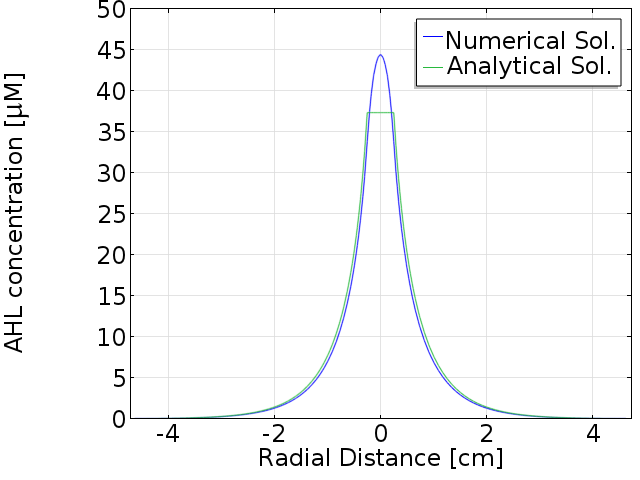
| + | <p align = "left"><b> Comparison with numerical solution </b></p> | ||
[[File:AHLss analytical.png|600px|center|thumb|<b>Figure 1:</b> Analytical approximation and numerical solution]] | [[File:AHLss analytical.png|600px|center|thumb|<b>Figure 1:</b> Analytical approximation and numerical solution]] | ||
Revision as of 14:17, 27 October 2013
Contents |
Steady State AHL Gradient Approximation
In the reaction-diffusion model we have formalized the gradient establishment and we solved the resulting partial differential equation numerically. Now, the aim is to derive a suitable analytical approximation for a single mine colony.
Kolmogorov-Petrovsky-Piskounov Equation
A reaction–diffusion equation concerning the concentration of a single molecule in one spatial dimension is known as the Kolmogorov-Petrovsky-Piskounov Equation. In our case, the equation for AHL has the following general structure:
\begin{align} \frac{\partial AHL(x,t)}{\partial t} = Diff(AHL(x,t),x) + R(AHL(x,t)) \end{align}
We were interested in the AHL gradient that can be established by a single colony ( located at $x = 0$) on an agar plate, ending up with a less general form of the reaction-diffusion model for AHL:
\begin{align} \frac{\partial AHL}{\partial t} = C_{agar} \cdot D_{AHL} \frac{\partial^2 AHL}{\partial x^2} - d_{AHL,e} \cdot [AHL] \end{align}
As boundary condition, we considered that the concentration at the mine colony stays constant, i.e. we are assuming cells are at the steady state:
\begin{align} [AHL](x=0,t) = [AHL]_{MineCell,ss} = \frac{\alpha_{AHL} \cdot [LuxI]_{ss}} {d_{AHL,i}+\eta \cdot \left(1-\frac{\eta_{ext}}{d_{AHL,e}+\eta_{ext}}\right)} \end{align}
Solution at the steady state
To solve the KPP equation for the steady state, we set to zero the time derivative:
\begin{align} \frac{\partial AHL}{\partial t} = C_{agar} \cdot D_{AHL} \frac{\partial^2 AHL}{\partial x^2} - d_{AHL,e} \cdot [AHL] = 0 \end{align} \begin{align} \frac{\partial^2 AHL}{\partial x^2} = \frac{d_{AHL,e}} {C_{agar} \cdot D_{AHL}} \cdot [AHL] \end{align}
This ordinary differential equation can be solved, integrating wrt. to x twice:
\begin{align} [AHL] = [AHL]_{MineCell,ss} \cdot e^{-\sqrt{\frac{d_{AHL,e}} {C_{agar} \cdot D_{AHL}}} \cdot x} \end{align}
Comparison with numerical solution
 "
"