Initial States

It is important to obtain the steady state concentration of molecules in our biological circuit, since these values can be used as biologically meaningful initial conditions for subsequent simulations. To achieve this goal, we implemented a Single Cell Model. The cells plated on the game plate are from an overnight liquid culture. Thus, we assume that the levels of the proteins of our engineered system in the cells have reached steady state.

Initial state for the Mine Cells

The mine colonies produce three molecules, NagZ, LuxI and AHL, that are important in our bio-game. The proteins NagZ and LuxI are constitutively produced, whereas the synthesis of AHL is dependent of LuxI. Moreover, degradation of these proteins is modeled as linear degradation. We have also taken into account the contribution on the dynamical evolution of AHL by diffusion toward/from the medium, distinguishing between intracellular and extracellular concentrations (Garcia-Ojalvo et. al., 2004.)

The ODEs for the states involved in the mine cells are given below:

\begin{align} \frac{d[LuxI]}{dt} =\alpha_{LuxI} - d_{LuxI} \cdot [LuxI]\\ \end{align}

\begin{align} \frac{d[NagZ]}{dt} =\alpha_{NagZ} - d_{NagZ} \cdot [NagZ]\\ \end{align}

\begin{align} \frac{d[AHL,i]}{dt}= \alpha_{AHL} \cdot [LuxI]-d_{AHL,i} \cdot [AHL,i] - \eta \cdot \left([AHL,i]-[AHL,e]\right)\\ \end{align}

\begin{align} \frac{d[AHL,e]}{dt}= -d_{AHL,e} \cdot [AHL,e] + \eta_{ext} \sum_{j=1}^{n} \left([AHL,j]-[AHL,e]\right)\\ \end{align}

System of differential equations for a sender cells, where $\eta = \sigma \cdot A/V_{c}$ measures the diffusion across the cell membrane, with $\sigma$ representing the membrane permeability, $A$ its surface area and $V_{c}$ the cell volume, and $\eta_{ext} = \delta/V_{ext}$ with $V_{ext}$ being the total extracellular volume.

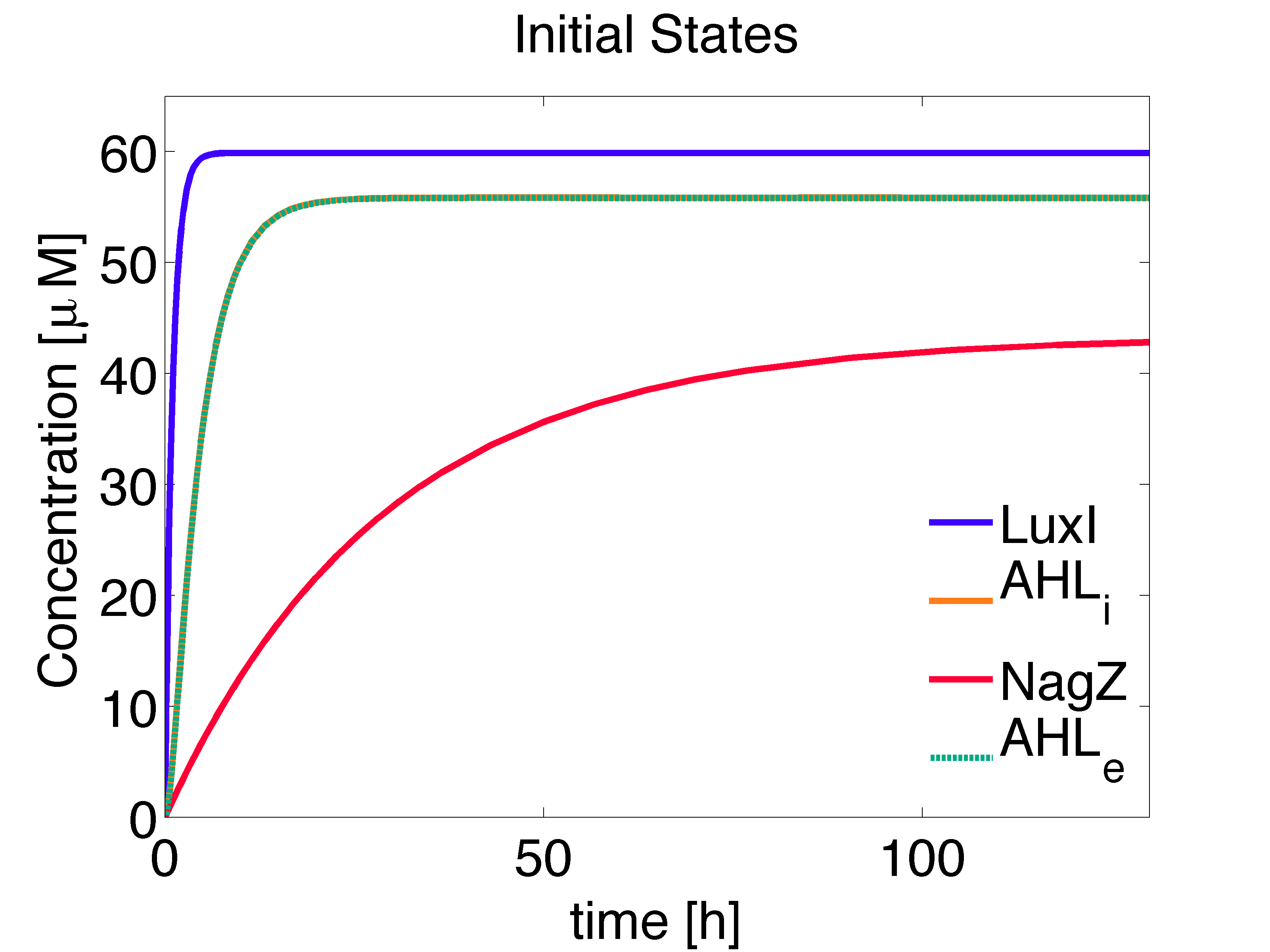
Figure 1: Steady state concentrations for Mine Cells

The concentration of the species at steady state can be solved analytically, obtaining solutions consistent with the numerical solution (Fig. 1):

\begin{align} [LuxI]_{ss} =\frac{\alpha_{LuxI}} {d_{LuxI}} \approx 59.8802 \mu M \end{align}

\begin{align} [NagZ]_{ss} =\frac{\alpha_{NagZ}} {d_{NagZ}} \approx 43.2809 \mu M \end{align}

\begin{align} [AHL,i]_{ss}= \frac{\alpha_{AHL} \cdot [LuxI]_{ss}} {d_{AHL,i} + \eta \cdot \left(1-\frac{\eta_{ext}}{d_{AHL,e}+\eta_{ext}}\right)} \approx 55.8492 \mu M \end{align}

\begin{align} [AHL,e]_{ss}= \frac{ \eta_{ext} \cdot [AHL,i]_{ss}}{d_{AHL,e} + \eta_{ext} } \approx 55.8291 \mu M \end{align}

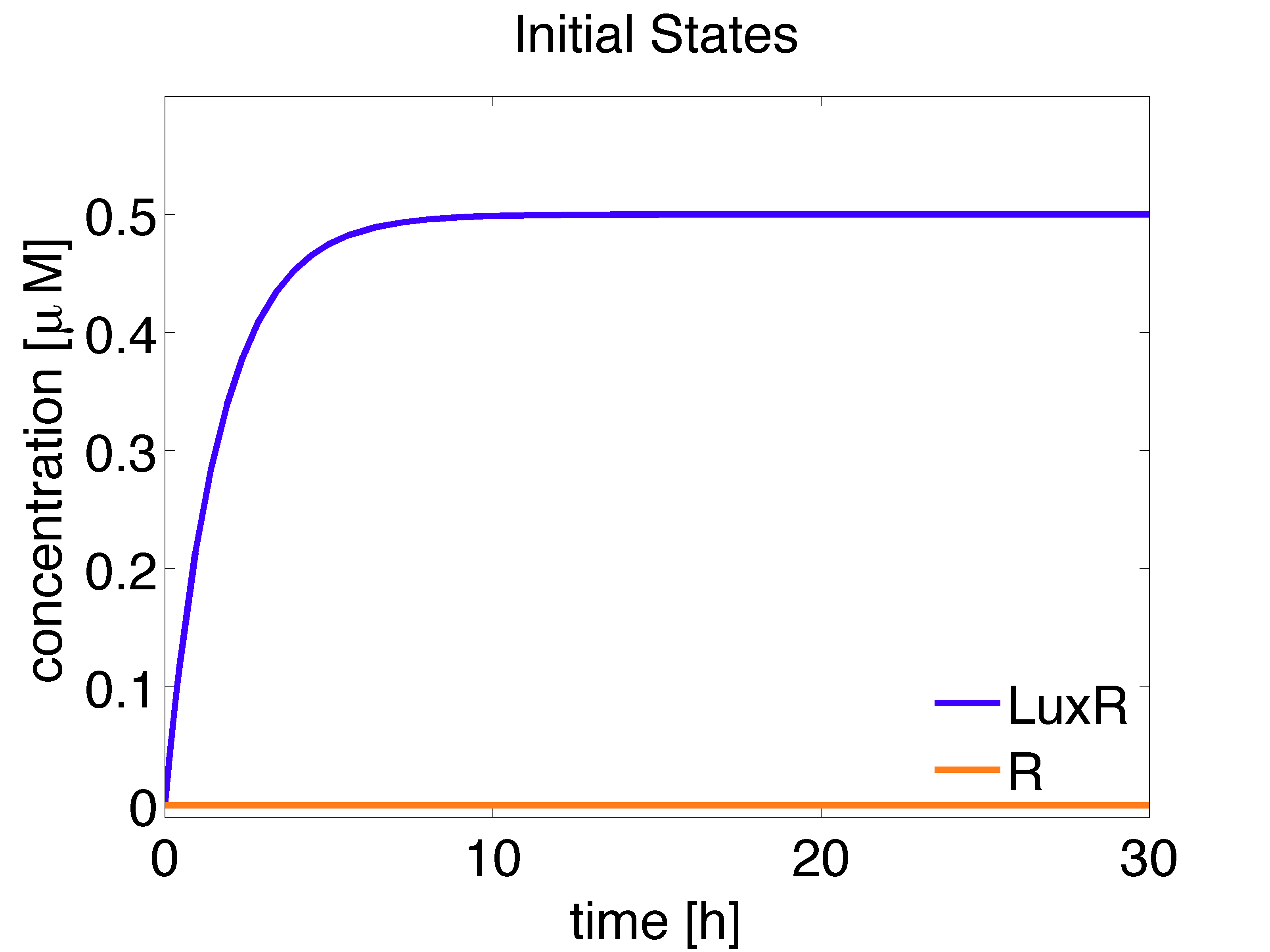
Initial state for the Receiver Cells

It should be noted that the receiver cells grow in the absence of AHL in the medium and this affects the concentrations of intracellular species whose production depends on AHL.