Team:NTU-Taida/Modeling/Flow Cytometry

Flow Cytometry

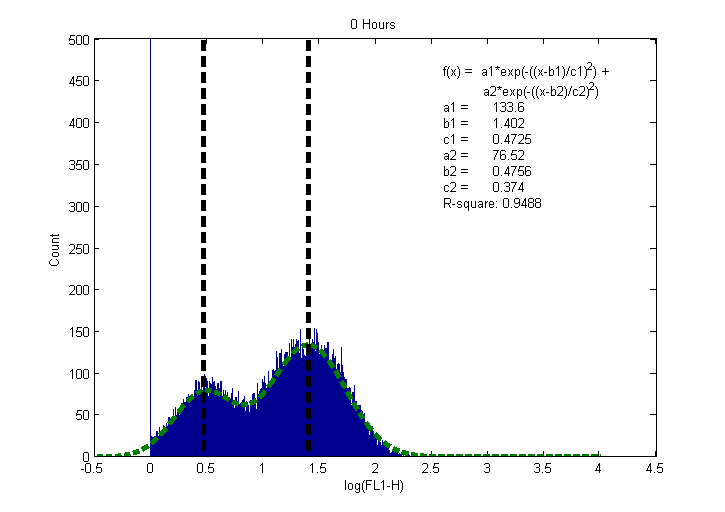
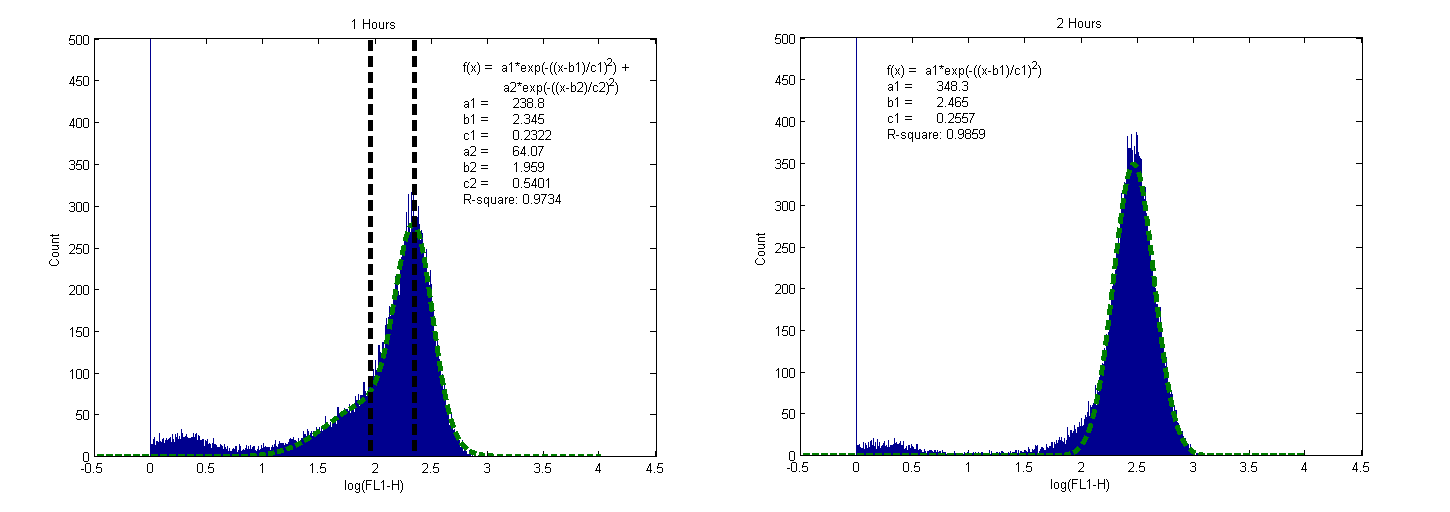
Now We try to find relationship between simulation result and reality by simulating the single cell model with Brownian noise many times (1000 times in this case) and collecting the data from flow cytometry (which can detect the GFP intensity of each cell and estimate the distribution of GFP intensity).

We collect the experiment result with 4 different initial condition (AHL concentration = 10^-3, 10^-5, 10^-7, 0) in 5 time points (0,1,2,3,4 hours after reaction) (Figure 1~4). Bi-Gaussian distribution are observed in some cases (with AHL concentration = 10^-3, 10^-5 ) at 1 hours indicated that positive feedback system were amplifying the signal. The cells which can trigger the positive feedback loop create more AHL receptor hence more GFP are generated and other cells which cannot trigger the positive feedback loop create GFP much slower ,yields Bi-Gaussian distribution. However the GFP intensity reach saturation within 1 hours in all cases.

Figure.1 GFP intensity distribution at time 0. (AHL injtial conc = 10^-5) Notice that it takes some time (15~20min) to prepare the sample for cell cytometry and the cell still detect AHL and produce GFP at this time.

Figure.2 (a) GFP intensity distribution at time 1hr. (AHL injtial conc = 10^-5). The cell reach max GFP intensity at this time. (b) The cell distribution of GFP intensity does not make any significantly change after 1hr

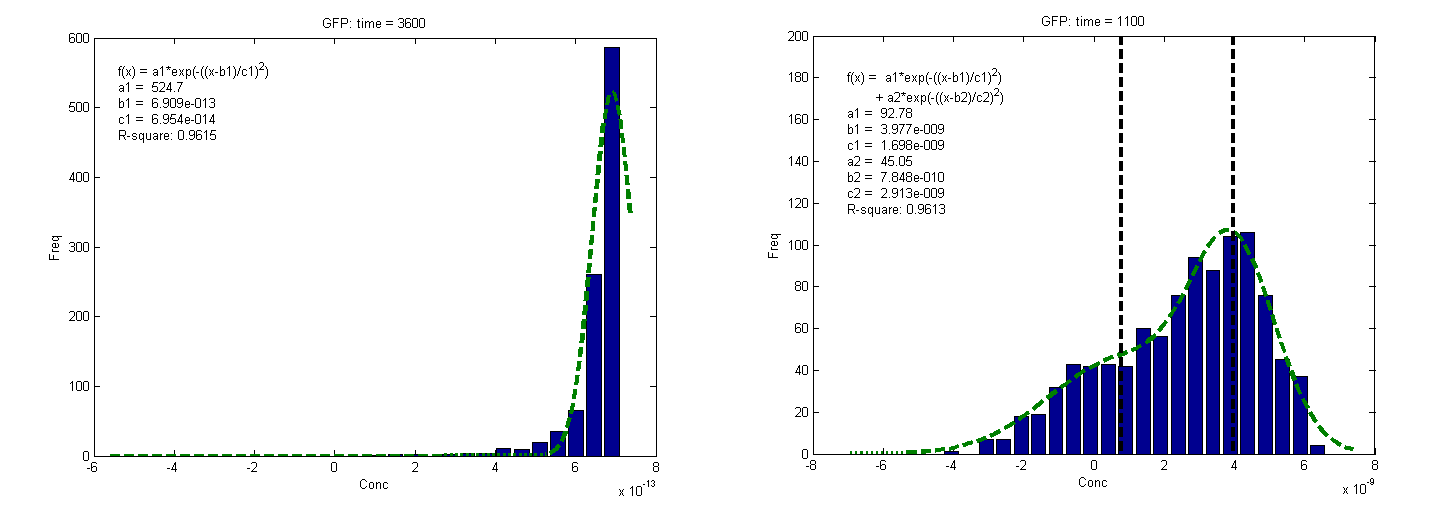
We have observed the similar behavior in our simulated data. The cell distribution are bi-gaussian in some initial condition at time 1100sec (compare with time 0 of real sample since the real sample need preparation to run flow cytometry), and the cell reach max GFP concentration within 1hr. (Figure 3)

Figure.3 Simulation Data (a)GFP intensity distribution at time 1100 seconds. (AHL injtial conc = 10^-5) This curve can be fit well by Bi-Gaussian Distribution (R² = 0.9613) (b) GFP intensity distribution at time 1hr. (AHL injtial conc = 10^-5). The cell reach max GFP intensity at this time.