Team:NTU-Taida/Modeling/Modified Simple Cell Model
From 2013.igem.org
Modified Simple Cell Model
We referenced and modified the model made by 2007 imperial iGEM team to our needs. This model simulate basic behavior of single cell, and assumptions are as follows:
- All molecules, including proteins, protein complexes and small molecules are uniformly distributed in cell bodies.
- The diffusion rate constant k16 of AHL is determined only by the AHL gradient between cytoplasm (denoted as [AHLi]) and extracellular matrix (denoted as [AHLe]).
- Initial [AHLi]=0, and [AHLe]=constant.
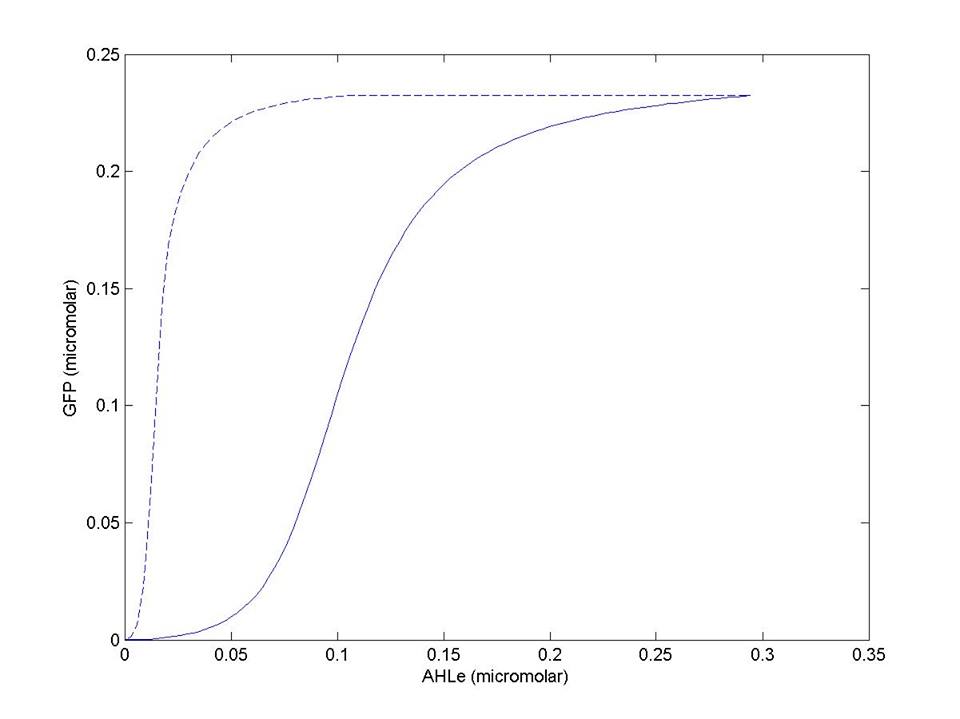
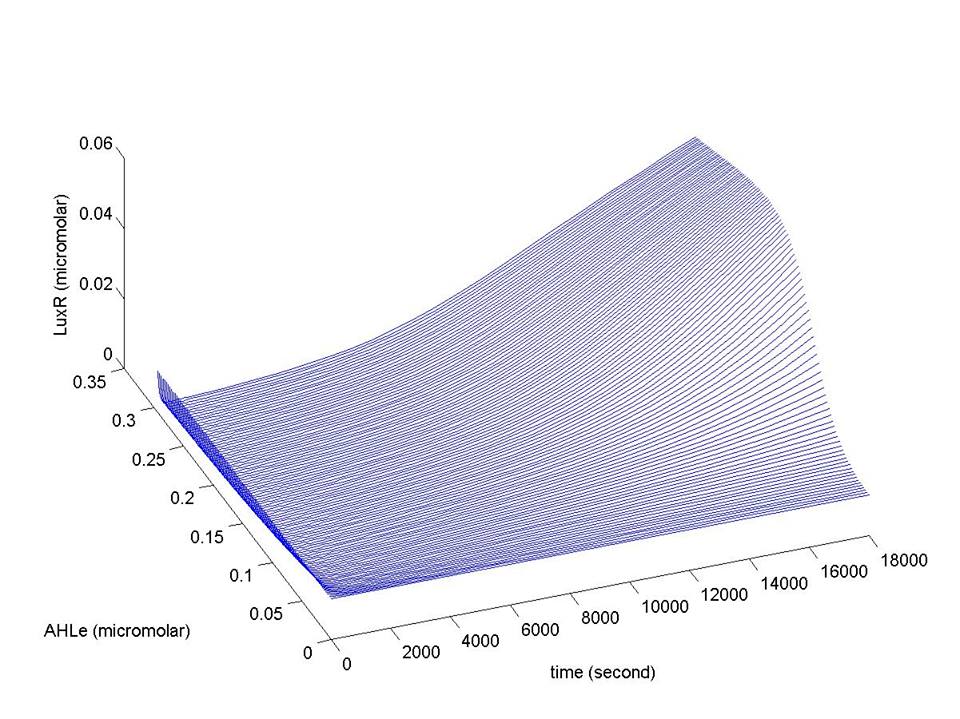
- LuxR protein ([LuxR]) is produced either by housekeeping gene which is assumed to have a constant transcription rate k1, or by positive feedback system discussed in 7. LuxR degrades with constant k12.
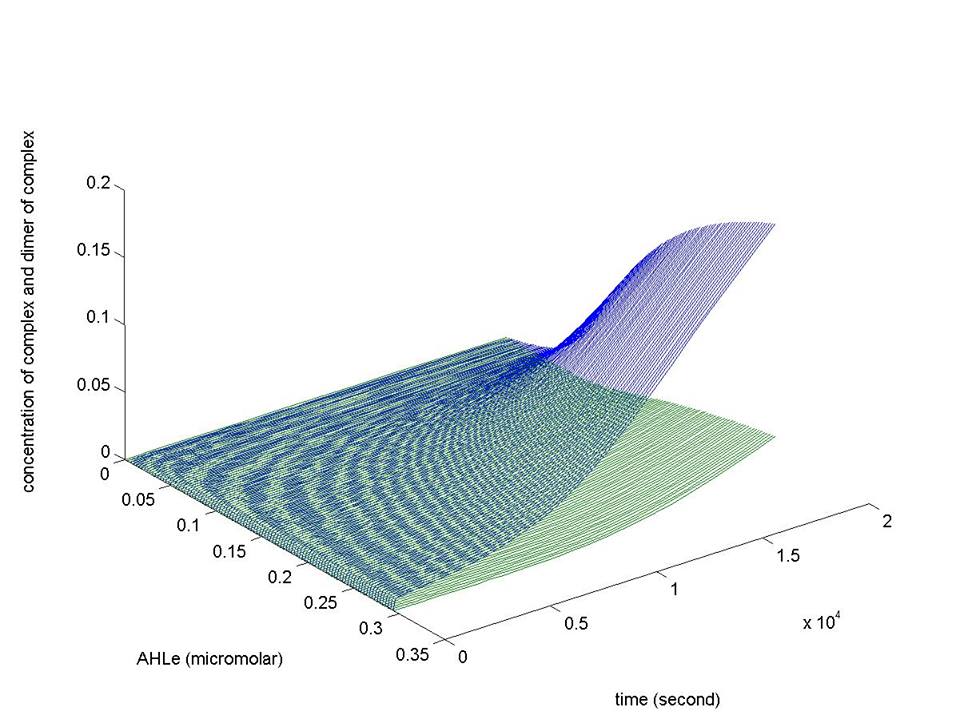
- AHL binds to LuxR protein, thus forming complex [C] at rate k5. The complex degrades into AHL and LuxR at rate k13.
- The aforementioned complex dimerize into dimer [D] at rate k6, and the dimer dissociates and forms two complex at rate k14.
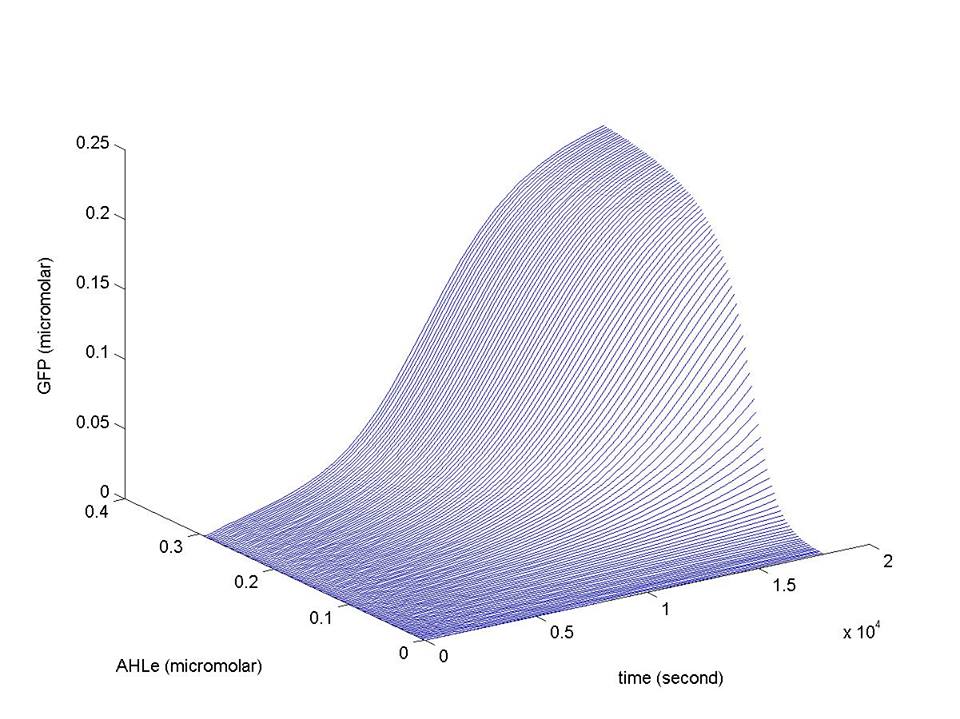
- The complex binds to inducible promoter of LuxR and GFP ([GFP]), which has three characteristics:
- The promoter complies to Hill's equation with cooperativity 1.
- Maximum transcription rate of this promoter is k2.
- Hill's dissociation constant is k3.
- The degradation rate of GFP is k18.
- Translation and degradation rate of mRNA is k4 and k11, respectively.
- Concentration of every species of molecules is adjusted for cell growth (dilution): $$ dxdt=−k8∗x5k9+x5∗x $$
- Parameters concerning bacterial growth:
- k7 is growth yield of bacteria
- k8 is maximum growth rate
- k9 is half-saturation constant
- k10 is bacterial death fraction per time
- [S] is nutrient in medium
- [N] is cell density
$$ d[N]dt=[N]⋅k8∗[S]k9+[S]−k10∗[N] $$
Implementation
We implement the model in MATLAB. Users can simulate this deterministic model many times with different rate constant (by specifying the standard derivation of constants).
 "
"