Team:ETH Zurich/Modeling/Reaction Diffusion OOHL
From 2013.igem.org
| Line 3: | Line 3: | ||
<h1>OHHL: Reaction-diffusion equations</h1> | <h1>OHHL: Reaction-diffusion equations</h1> | ||
| - | <p align="justify"> '''Modeling the | + | <p align="justify"> '''Modeling the AHL diffusion-reaction is a vital aspect of our biogame, because It played an important role in determining the geometry of the game field and the timing. '''<br></p> |
<br clear="all"/> | <br clear="all"/> | ||
Revision as of 11:34, 19 October 2013
Contents |
OHHL: Reaction-diffusion equations
Modeling the AHL diffusion-reaction is a vital aspect of our biogame, because It played an important role in determining the geometry of the game field and the timing.
Video: 2D gradient formation over 24 hours, starting from OHHL steady state concentration in the mine colonies.
Display: OHHL concentration in mol/m3. Distance between colonies: 1.5 cm.
The change of OHHL concentration over time is influenced by two processes: (i) local chemical reactions and (ii) diffusion; which causes the molecule to spread radially through the agar. (Eq. 1).
For diffusion, we have a partial differential equation (Eq. 2) which describes density fluctuations over time and space (r=(x,y)). We do not model OHHL diffusion in and out cells explicitly; the underlying assumption is that this process is fast or that the molecule diffuses freely. In equation 2, DOHHL(OHHL(r,t),r) denotes the collective diffusion coefficient for OHHL at location r. However, we assume that the diffusion coefficient does not depend on the density, i.e., DOHHL is a constant. The value reported in the literature for the diffusion constant corresponds to measurements performed in water at 25oC. As the OHHL in our system diffuses in agar, we scaled the diffusion constant by a factor Cagar (Fatin-Rouge et al., 2004).
For the reaction component, the change of OHHL concentration over time is modeled by a set of ordinary differential equations (ODEs), that includes the production and linear degradation or decay. However, the types of reactions that take place depend on the localization, i.e. extracellular or cytoplasmic. In the case of cytoplasmic localization, we have to further distinguish between the two type of cells encountered in our system, sender cells and receiver cells. Mine cells synthesized the signalling molecule which depends on the product of luxI gene, while for the degradation we assumed a linear dependency of the molecule concentration. For the receiver cells only linear degradation take place, and we assume that is under the same rate as mine cells. However, for the extracellular decay we consider that OHHL degrades at a different rate, because the intracellular process is driven by enzymatic degradation, whereas the extracellular decay is a non active process. Furthermore, we include a dilution factor to account for cell growth modelled using the logistic equation (Eq. 3). It is important to point out that, the growth rate was obtained from experiments.
Finally, we need to specify initial conditions (at time t = 0) and boundary conditions. At the starting point there is no OHHL in the agar plate, thus the initial concentration is zero ([OHHL](r,t=0) = 0 M) for receiver colonies and in the agar plate. However, the initial concentration in the mine colonies was set to the steady state concentration, which was obtained from a single cell model. For the boundary condition, we take into account that there is not flux out of the agar plate.
RESULTS: Simulation
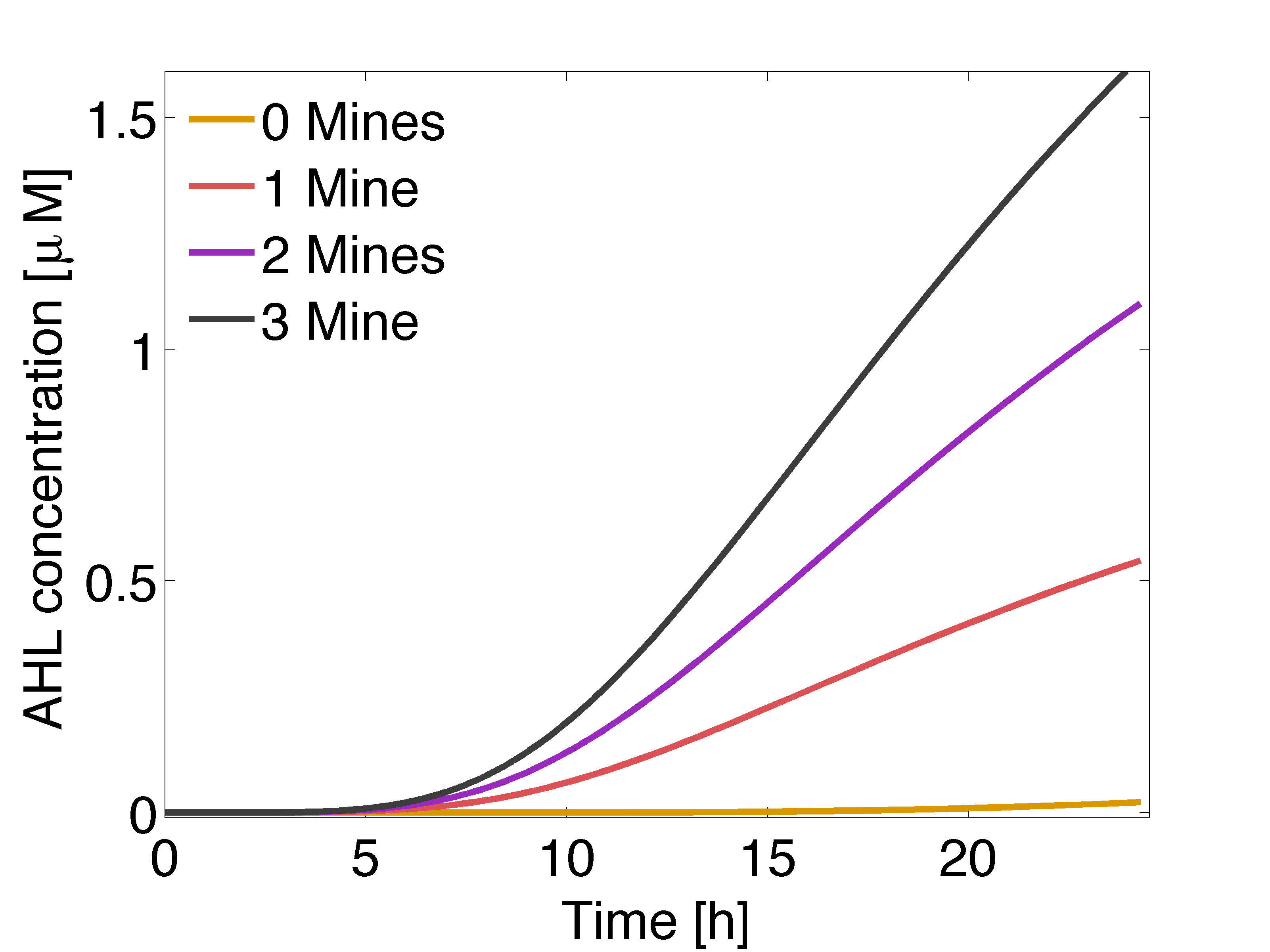
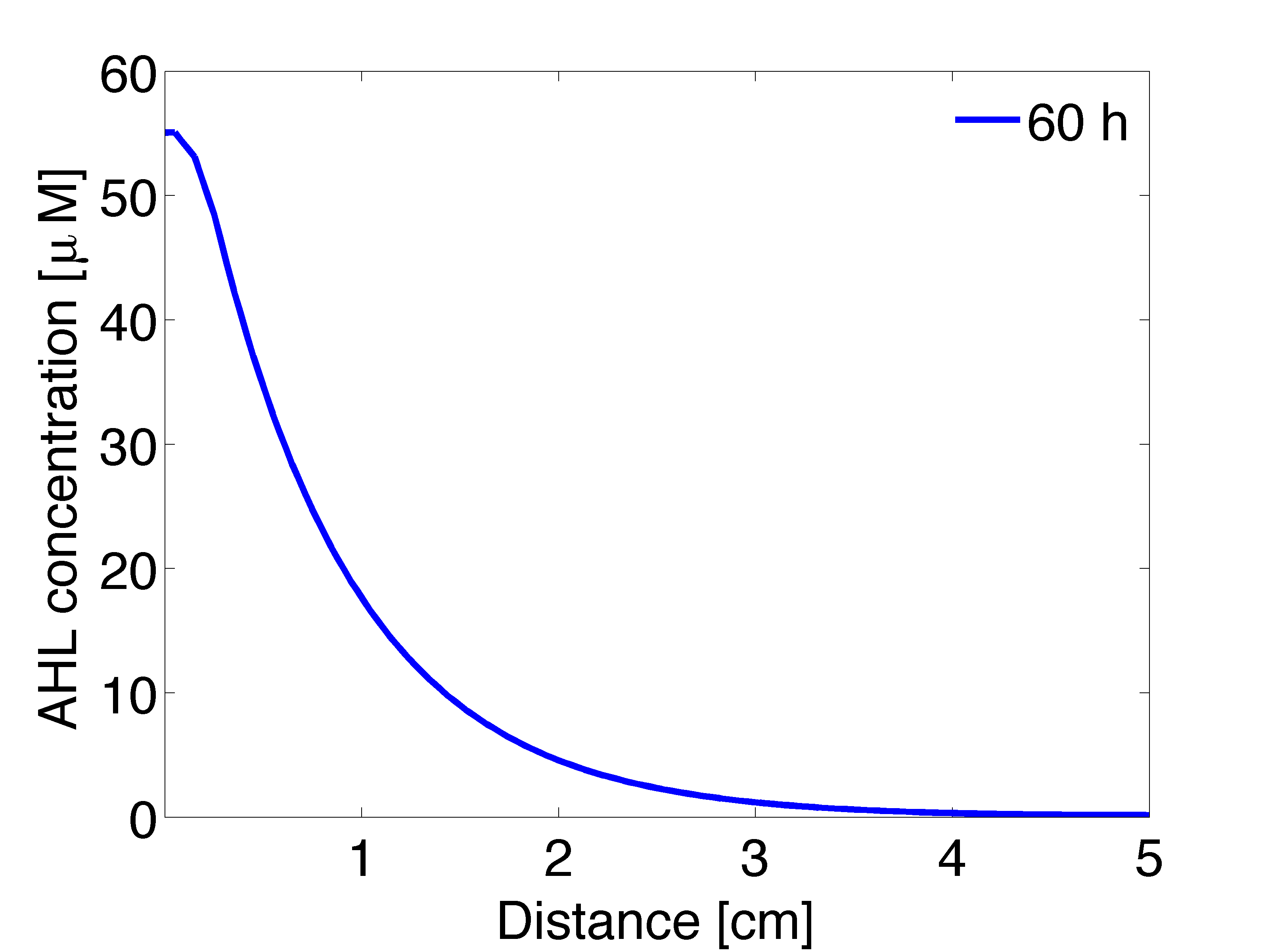
In figure 1 is displayed the time course of the averaged concentration of OHHL for colonies surrounded by 0, 1, 2 or 3 mine colonies. The steady state concentration versus distance for OHHL concentration derived from a 1D spatio-temporal model is displayed in Figure 2; the stationary solution is achieved after 60 hours
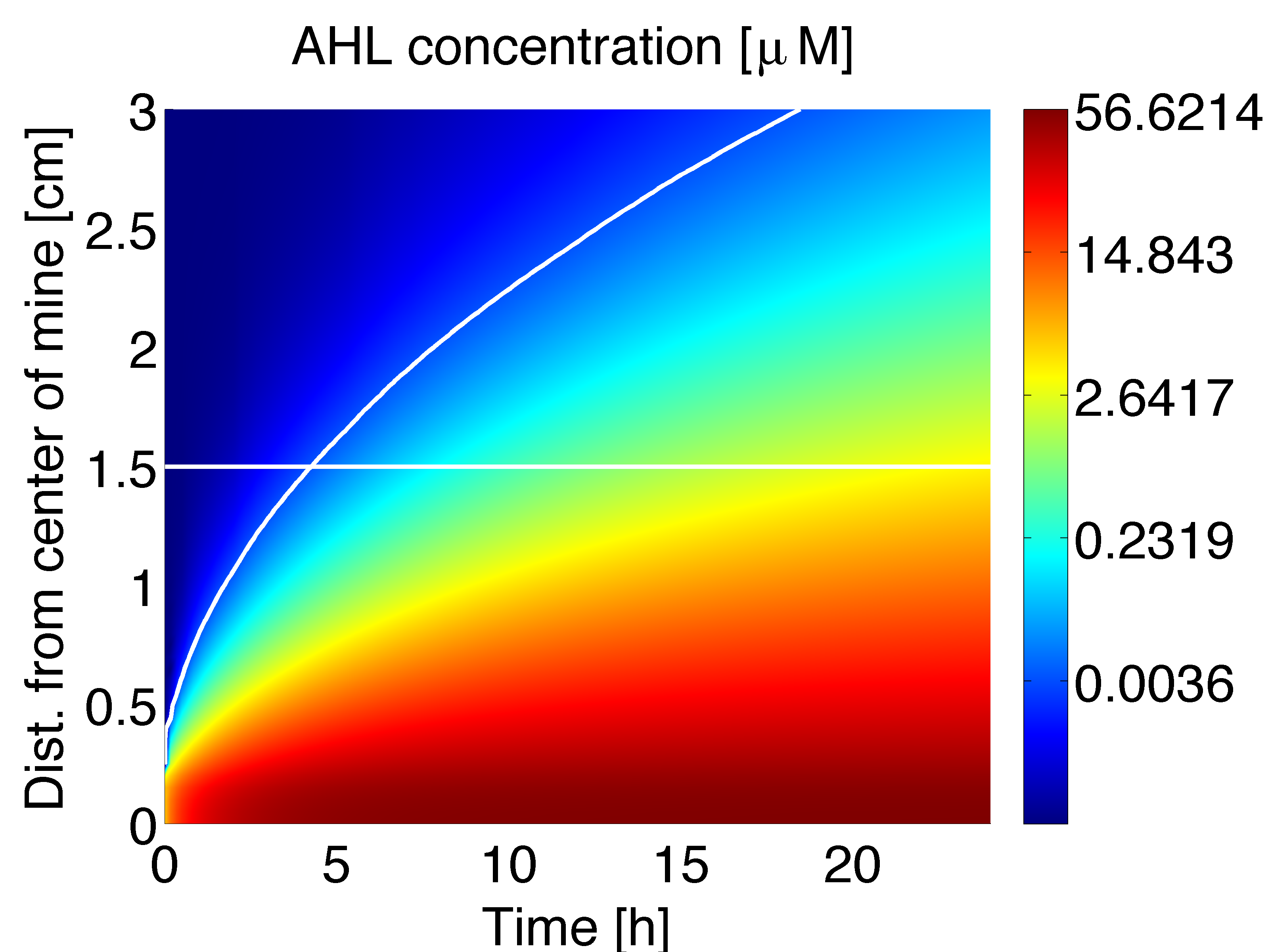
From figure 1 important conclusions can be drawn. Before 5 hours it is expected to have non-differential activation due to LuxR/OHHL complex, because the OHHL concentration at the receiver colonies is nearly the same independent of the number of neighbouring mine colonies. This prediction can be supported by the intersection of the 50% PLuxR promoter activity curve and the distance between the colonies in figure 3. After 6-7 hours the difference in activation due to LuxR/OHHL complex should start to be significant and remain over time. However after 18 hours, colonies that are further apart from mine colonies, they start to be exposed to OHHL.
The model predicts that mine colonies are able to generate a suitable gradient by synthesizing OHHL at a sufficient rate to overcome the decay and the active degradation; the gradient is suitable because receiver colonies are exposed to different concentrations of OHHL, depending on the number of adjacent mine colonies.
It is important to point out that for the design of the game grid, model and diffusion experiments lead to a working geometry (hexagonal honeycomb), distances (1.5 cm between colonies) and timing (11 hours incubation for the plates).
Growth curve fitting
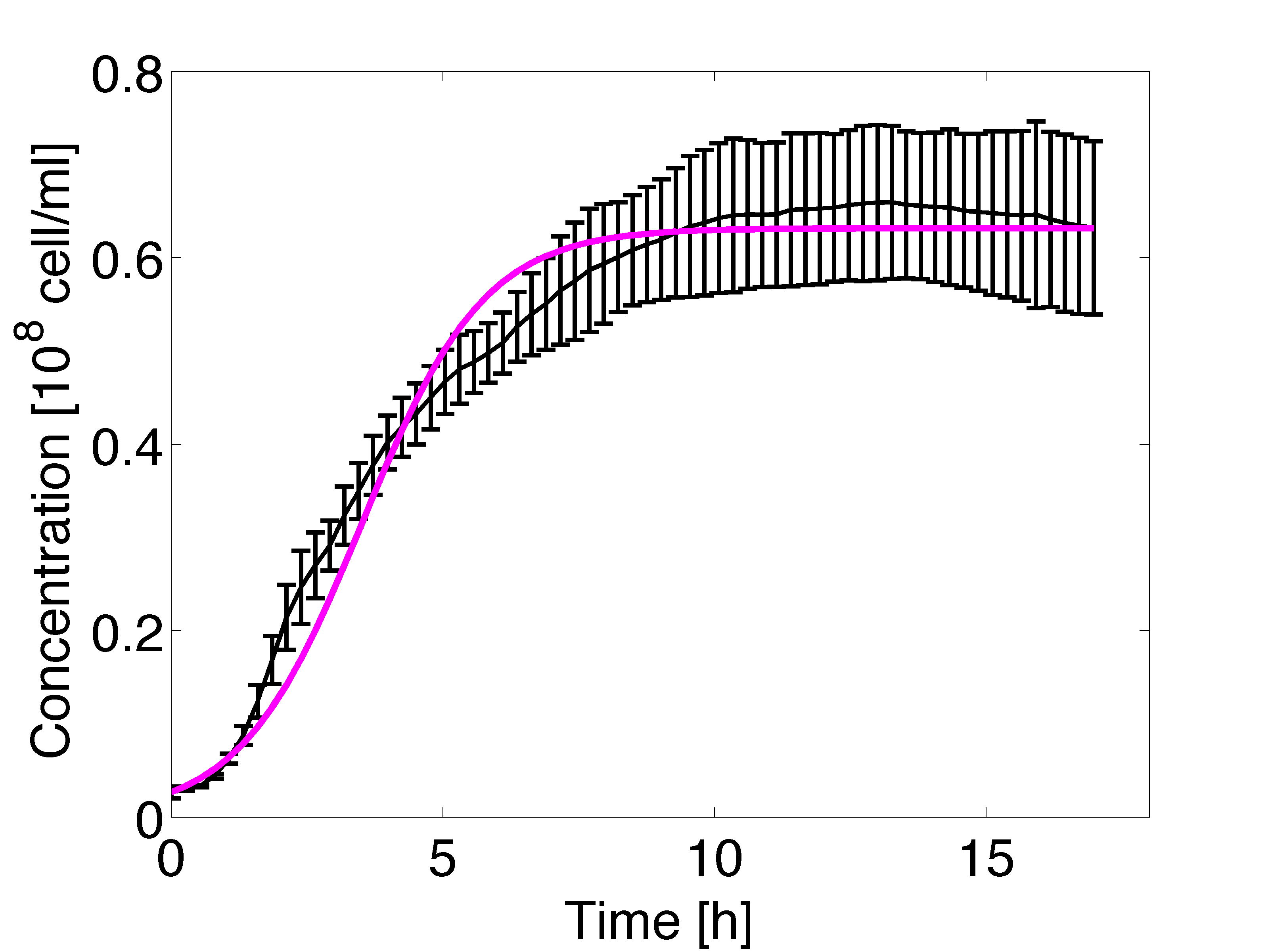
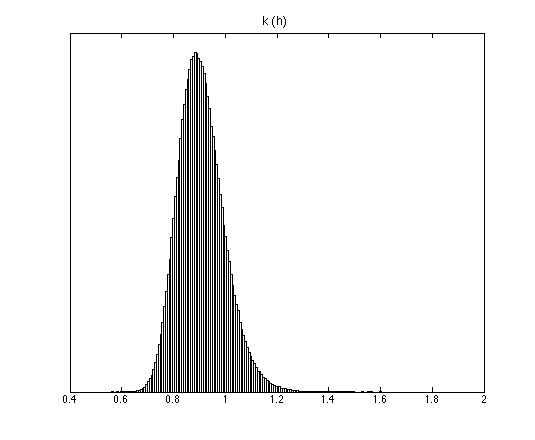
The estimation of the growth rate parameter was carried out using a mcmc variant, Delayed Rejection Adaptive Metropolis ([http://helios.fmi.fi/~lainema/dram/ DRAM]).The optical density measurements were conducted in triplicate over 17 hours, results are shown in figure 4 and 5. This parameter was incorporated in the model.
 "
"